Beyond the Monad fashion (I.): Writing idioms in LINQ

Thanks to LINQ and Erik Meier, monads have become a fashionable topic in the C# developer community. Indeed, no serious developer conference on .NET can get away without having a talk on monads. The attractive thing about LINQ and monads is that the SelectMany operator roughly corresponds to the bind function that defines a monad. In practice, LINQ is used for working with collections of data (IEnumerable<T>), but you can also define bind (i.e. SelectMany) for some other data types and use the LINQ syntax for working with other types. You won't be really using the full LINQ syntax. You'll probably use just nested from clauses (for binding) and select at the end to return the result.

However, monads are not the only notion of computation that we can work with. More interestingly, they are also not the only notion of computation that you can encode using LINQ! In this article, I'll briefly introduce idioms (also called applicative functors), which is another useful abstract type of computations. Idioms can be used for a few things that cannot be done using monads.

A provocative summary of this article is: "Everyone who tells you that LINQ is a monad is wrong!"

The truth is that LINQ syntax can be used for encoding queries (obviously), monads (as you were told), but also for idioms as you'll learn today (and quite possibly for other types of computations). In this article, we look at a basic example, but I'll describe a more complex real-world scenario in the next blog post.

Monads and LINQ

To set the scene, we I briefly demonstrate the encoding of monads using LINQ. You can find similar examples in quite a few blog posts on the internet (and at any serious .NET conference these days). I covered the topic in detail in my Real-World Functional Programming book. The Chapter 12 which explains monads and LINQ is available for free as a sample chapter [5].

The example I used in the book uses values of type Option<T>. The value can either contain a value of type T (Option.Some) or it can be empty (Option.None). It is similar to Nullable<T> with the only difference that the contained value can also be a reference type). When working with options, you can use LINQ syntax to write computations that can fail and return Option.None at any time without explicitly checking for it:

var res = from n in TryReadInt()
          from m in TryReadInt()
          select n + m;

The sample tries to read number from the console (TryReadInt). If the user enters two valid numbers, the result will be Option.Some containing the sum. However, if the user enters wrong input, the rest of the computation will not run and the result will be immediately Option.None.

Introducing idioms

Monads are certainly very nice, but as I wrote, they are not the only notion of computation that we can use. In this article, we'll look at idioms, but there is quite a few of them (another interesting example is comonads; you can find a short Haskell introduction here [1]). Idioms are particularly interesting because they are closely related to monads. They are weaker than monads, which means that all monads are idioms, but not all idioms are automatically monads. Let me first quote Conor McBride and Ross Paterson who described idioms and I'll clarify everything shortly:

The moral is this: if you’ve got an Applicative functor, that’s good; if you’ve also got a Monad, that’s even better! And the dual of the moral is this: if you want a Monad, that’s good; if you only want an Applicative functor, that’s even better!

In the object oriented terms, you can think of idiom and monad as two interfaces. The monad interface inherits from the idiom interface. When you write some method, you'll prefer to take idiom as an argument (because this means that your method can work with more objects). If you're defining a class, you'll prefer to implement monad, because it means that your object can be passed even to methods that have stronger requirements (that require monad and not just idiom).

Defining an idiom

Both monads and idioms are defined in terms of a few simple operations that they need to provide. For monads, one of the operations is Bind (which is similar to SelectMany in LINQ) and the other operation is Return (it doesn't have a direct correspondence in LINQ, but imagine you could write var q = select 10 to create a list containing a single value 10).

The operations that are required by idiom are Return (just like for monads), Select (which happens to be the same thing as Select in LINQ) and Merge (in the academic terminology, they are usually called unit, map and ★). The operations should have the following types (I'm using the F# syntax, so -> stands for the Func delegate or a method):

// Operations required by a Monad
Return : R -> Monad<R>
Bind   : Monad<T> -> Func<T, Monad<R>> -> Monad<R>

// Operations required by an Idiom
Return : R -> Idiom<R>
Select : Idiom<T> -> Func<T, R>) -> Idiom<R>
Merge  : Idiom<T1> -> Idiom<T2> -> Idiom<Tuple<T1, T2>>

The Return operation does the same thing as Return for monads. It turns an ordinary value into a value wrapped inside idiom. This could mean a different thing for a different type of computations. For option values from the introduction, we could wrap the value using Option.Some.

You may already have some intuition about Select from LINQ. It should turn all values inside one idiom into different values (using the provided function) and wrap them inside an idiom with the same structure. For options, we would turn Option.Some into Option.Some containing the calculated value; for lists, we would apply the function to all elements of a list.

The Merge operation is the key thing. It takes two idioms and combines them into a new idiom that contains two-element tuples. The first element is some value from the first idiom and the second value comes from the second idiom. If you carefully look at all the Enumerable members in the MSDN documentation, you'll find a method that has a very similar signature. You'll find out which method I'm talking about in the next section when we define our first idiom...

Writing our first idiom

There are two ways to define an idiom for IEnumerable<T>. As already mentioned, when you have a monad, you also automatically get an idiom. I'll show you how to do that later, but it is possible to implement Merge in terms of Bind. In that case, the Merge operation will behave essentially as cross-join, which means that it generates all combinations of the elements from the two sequences. For example, if you have [1; 2] and [a; b; c] you'll get [1,a; 1,b; 1,c; 2,a; 2,b; 2,c]. This isn't a very interesting example, because we can do that with monads. However, there is another option...

Implementing ZipList idiom

The alternative implementation is to use the Zip operation as Merge. The Zip operation [3] takes two collections and generates a new one by taking elements at the corresponding indices. If you have [1; 2; 3] and [a; b; c] you'll get [1,a; 2,b; 3,c]. There is only a single sensible way to implement the Select and that's to use the same behavior as LINQ. However, the Return operation may be surprising. Let's look at the three methods:

// Returns an infinite sequence containing the specified value
public static IEnumerable<T> Return<T>(T value) {
  while (true) yield return value;
}

// Merges corresponding elements from two sequences into tuples
public static IEnumerable<Tuple<T1, T2>> Merge<T1, T2>
    (this IEnumerable<T1> first, IEnumerable<T2> second) {
  return Enumerable.Zip(first, second, Tuple.Create);
}

// Applies the specified function to all elements of source 
public static IEnumerable<R> Select<T, R>(this IEnumerable<T> source, Func<T, R> func) {
  foreach(var el in source) yield return func(el);
}

In the usual List monad (that roughly corresponds to LINQ), the Return operation returns a single-element sequence that contains the specified value. However, for the ZipList idiom, we need a different behavior. When we look at some examples, you'll see that this implementation allows us to write useful things just using the idiom operations. Another reason is that idioms should obey some laws to give a reasonable definition. You can think of laws as unit tests that should hold for any random input. One of the laws about Return is:

[Test]
public void LeftIdentity<T>(IEnumerable<T> source) {
  Assert.AreEqual( source, source.Merge(ZipList.Return(0)).Select(tup => tup.Item1) );
}

Common unit testing frameworks wouldn't be able to randomly generate values for the argument, but you get the idea. The law says that if you Merge any sequence with a sequence generated using Return and then take only the first element of the tuple, you should get the same thing as the original sequence. This is something that sounds obvious, but it wouldn't work if we used Return that generates only a single element.

Programming with ZipList

Now that we have idiom for ZipList, let's see how we can use the provided operations to solve some problems. We'll start with a basic example that calculates average price of stock prices over several days that are stored in sequence of sequences:

// Changing prices of 4 different stocks over 3 days
var prices = new[] { 
  new[] { 10.0, 4.0, 13.0, 20.0 },
  new[] { 12.0, 3.0, 11.0, 25.0 },
  new[] {  9.0, 1.0, 16.0, 24.0 },
};

// Calculate average price for each stock
var res = ZipList.Return(0.0);
foreach (var day in prices)
  res = res.Merge(day).Select(tup => tup.Item1 + tup.Item2);
var avg = res.Select(sum => sum / prices.Count());

// Print results: 10.3, 2.6, 13.3 and 23 
foreach (var price in avg)
  Console.Write("{0}, ", price);

How does the calculation of the average work? We first need to sum all prices over the three days. To do that, we add prices for all days to the current sum in a foreach loop. To add values, we Merge the results so far with the prices for the current day and then use Select to add them. As an initial value, we use a sequence containing zeros generated using Return. A nice thing is that we don't need to explicitly specify the length of the sequence, because Merge can take as many zeros from it as needed.

This was a fairly simple example, but we'll look at a more complicated one later. First of all, let's look how LINQ fits into the picture.

Writing idioms using LINQ

The LINQ query syntax doesn't provide any direct way for encoding idioms. However, we can misuse one of the standard query operators for this purpose. There aren't many benefits in a simple example like this one. In the next blog post, we'll look at a larger example and the syntax will be quite useful. The keyword that we can misuse is join:

var res = ZipEnumerable.Return(0.0);
foreach (var day in prices)
  res = from sum in res
        join price in day on 1 equals 1
        select sum + price;
var avg = from sum in res select sum / prices.Count();

When using join for implementing actual database joins, we can specify keys that should be matched using the equals clause. When encoding idioms, we just ignore the clause, so I'll always write just on 1 equals 1. The reason why we can use join for encoding idioms is because it is translated to Join calls in a way that's very similar to what we need to write when using Merge directly (You can find more details in the C# specification [4]). The key difference is that you cannot use variables declared earlier in the query (e.g. sum) in the expression that specifies data source for joining (e.g. day).

How does it work?

When working with idioms, we cannot select data source depending on a value from previous data source. This essentially means that all the data sources used by one or more join clauses and the first from clause will be combined using Merge. Then the query will use Select to evaluate the expression specified in select. This is different than monads encoded using multiple from clauses where the next from expression can depend on earlier variables. For example, when using monads, you can write:

var q = from cat in RandomCategories()
        from prod in ProductsInCategory(cat.ID)
        select prod.Name;

Note that we can use the cat value in the in part of the second from clause. This is because the translation that C# uses for multiple from clauses and the translation used for join is very different (and the variable simply isn't in scope when using join). Because of the translation, the Join method also has quite different type than the SelectMany method (used by monads). If you write the declaration of the Join method (and decide to ignore the two key selectors), you can easily find a way to implement it in terms of Merge and Select provided by any idiom:

// Allows using of the join keyword for writing idiom computations
// (they two key selectors are ignored and users can just write 'on 1 equals 1')
public static IEnumerable<TResult> Join<TOuter, TInner, TKey, TResult>
  (this IEnumerable<TOuter> outer, IEnumerable<TInner> inner,
    Func<TOuter, TKey> outerKeySelector,
    Func<TInner, TKey> innerKeySelector,
    Func<TOuter, TInner, TResult> resultSelector) {

  // Implementation using just 'Merge' and 'Select'
  // that can be provided by any idiom
  return outer.Merge(inner).Select(tup => resultSelector(tup.Item1, tup.Item2));
}

In fact, the implementation could just directly use Enumerable.Zip. However, I wanted to write it explicitly using Merge and Select, because these two are the operations used to define idioms in the original paper about idioms [1] (In fact, the paper gives two equivalent definitions and I'm using the second one, because it is easier to understand).

If you want, you can look at the query translation [4] and try to rewrite the LINQ query above (or use Reflector or similar tools) to see how the C# compiler desugars the query. However, the fact that we could directly implement Join (without key selectors) using operations from an idiom means that the computation is using just operations of the idiom (in some way) and that the code is equivalent to what we wrote earlier explicitly.

Transposing matrices with idioms

One example of using idioms that you can find in the original paper [1] is matrix transposition. We can implement that using our ZipList idiom and the encoding using LINQ as well. The implementation won't be very efficient (it was designed to work with lazy functional lists), but it is an interesting demonstration. In the next blog post, I'll show you how to implement a more real-world idiom, so the purpose of the example isn't to convince you that writing idioms using LINQ is a good idea - instead, I just want to demonstrate that we can rewrite any example from the original article. The following method implements the transposition using the LINQ syntax for idioms:

IEnumerable<IEnumerable<T>> Transpose<T>(this IEnumerable<IEnumerable<T>> matrix) {
  return matrix.Count() == 0 ?

    // Processed all rows - return infinite sequence of empty lists
    ZipList.Return(Enumerable.Empty<T>()) :

    // Zip all elements from the first row 'matrix.First()' with rows of 
    // recursively transposed sub-matrix starting from the second row
    from xs in matrix.First()
    join xss in Transpose(matrix.Skip(1)) on 1 equals 1
    select Enumerable.Concat(new[] { xs }, xss);
}

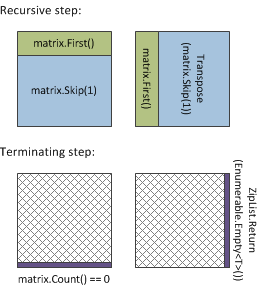
This function is a bit tricky, but you can understand it by looking at the diagram on the right. We start processing the matrix by taking the first row. Then we take a smaller sub-matrix that with the first row removed (matrix.Skip(1)) and transpose this sub-matrix. Once we have these two, we use ZipList idiom to merge individual columns of the first row and rows of the transposed matrix back together.

When we eventually reach the end, we need to generate a sequence that is at least as long as the height of the matrix. The sequence (representing rows) should contain empty sequences (representing columns) so that we can later append elements to the individual columns (using Enumerable.Concat).

If we wanted to write the same thing explicitly using the idiom operations, we'd just need to change the else clause of the conditional operator and use the following:

ZipList.
  Merge(matrix.First(), Transpose(matrix.Skip(1))).
  Select(tuple => Enumerable.Concat(new[] { tuple.Item1 }, tuple.Item2));

As I already mentioned, the difference between the two syntactic options isn't as huge in this basic example. The main benefit of (mis-)using the query syntax is that we can avoid using tuples explicitly, which makes our life a bit easier. In this example, we're merging just two inputs, so the tuple is quite simple. In the next blog post, we'll need to merge a much larger number of idioms, so the code would look quite ugly and we'd have to work with tuples like Tuple<string, Tuple<Unit, Tuple<Unit, string>>>.

Summary

The LINQ query syntax in C# is quite a powerful weapon. Obviously, it can be used for encoding queries, but you can use it to write other types of computations as well. There are quite a few blog posts and articles (including freely available Chapter 12 of my book [5] that explain how to use LINQ syntax for working with monads.

However, saying that LINQ is a monad isn't quite right, because the LINQ syntax can be used for encoding other types of computations too. In this article, I demonstrated how to use it for writing code using idioms. Idioms are weaker than monads - in the object oriented terms, this means that the "monad interface" inherits from "idiom interface". As a result, some computation types can implement the "idiom interface", but cannot be written as monads. We looked at ZipList, which is one example of such computation type.

I demonstrated how you can use (somewhat surprisingly) the join clause to work with idioms and we also looked at some examples. You've seen matrix transposition which is one of the examples used in the original paper that introduces idioms.

The ZipList example may look a little academic, but it was quite easy to explain. If you want to see a more practical example, stay tuned for the next blog post. I'll demonstrate using Formlets [6], which is an idiom that can be used for constructing web forms.

References

• [1] Applicative programming with effects (PDF) - Conor McBride, Ross Paterson
• [2] I understand comonads - Bloggy Badger
• [3] Enumerable.Zip<TFirst, TSecond, TResult> Method - MSDN Library
• [4] Query Expression Translation - C# Overview - MSDN Library
• [5] Chapter 12: Sequence expressions and alternative workflows - Real-World Functional Programming
• [6] The essence of form abstraction - Ezra Cooper, Sam Lindley, Philip Wadler, Jeremy Yallop