Solving fun puzzles with F#
Do you need to convince your friends & family that programming can be fun? For the last Christmas, I got a puzzle as a gift. It is a number of small cubes, joined together, that can be rotated and folded to form a bigger (4x4x4) cube.
We spent the last few days of the year with family and a couple of friends and I left the puzzle on the table. Every time I walked around, someone was playing with it without much success. In the end, I said that if noone solves it until 31 December, I'll write a program to do it. Which I did between 7 PM and 8 PM and, voilà, here is what I got...
So, how do you solve a puzzle in about 1 hour on New Year's eve?
Modeling the problem
As with any problem in F#, we start by modeling the domain. The puzzle consists of parts (small cubes) that have two important properties:
1: 2: 3: |
|
Each part has a color (black or white) and there are two kinds of parts. In one kind, the string connecting the parts goes straight through the part (and so it does not allow any useful rotation). In the other part, the string turns and so the next part can point in one of four directions. Assuming the previous part points from bottom to the top, we can now go to the front, back, left or right.
We'll also need to represent positions of the parts in the final cube and the direction in which a part is pointing:
1: 2: |
|
Here, the position will be integers from 0 to 3 and direction will always contain exactly one 1 or -1 value (with zeros for all other axes). We could make the model more precise, but this will make calculations easy (note that we only have 1 hour to finish :-)).
Now, the entire puzzle (first picture) is simply a list of parts:
1:
|
|
The model so far can actually be understood by non-programmers. It has been tested on humans (but only close relatives and friends!) and it worked fine :-). This is one of the key strengths of domain modeling with F#...
Implementing the algorithm
The algorithm we'll implement is quite straightforward backtracking. We'll simulate the different ways in which the puzzle can be folded (starting from 4 different positions as others would be symmetric). When we hit a state that would not be valid (there is a part already or the colors would not match), we'll go back and try another folding.
When we have a Straight part, the next part of the puzzle will always be one
step further in the current direction. This is easy. The interesting thing is
when we have a Turn part - in that case we can go in four different directions,
which are calculated using the following functions:
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: |
|
To understand this part, you still do not need to be a programmer. And the fact that we are writing just functions makes this quite easy too. However, you definitely need some mathematical background.
Checking valid moves
The next part of the preparation is to write a function for checking whether a move is valid. There are two conditions:
- A move is not valid if there is a part already at a given
Position. - We can only put parts inside the range of the cube (all coordinates are within 0 .. 3)
- The colors of the parts should match the pattern that you can see in the picture above.
We'll keep a set of occupied positions using immutable F# Set. For color
patterns, we can build a simple dictionary with expected colors - as the
pattern is regular, we can only store colors for smaller 2x2x2 cube (and then
check using pos / 2.
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: |
|
The following isValidPosition function takes a Position and a current CubeState
and checks whether it is a valid position (we'll handle colors later):
1: 2: 3: 4: 5: 6: 7: 8: 9: |
|
This ignores the color constraints. Mainly because I added this later when solving the puzzle. Surprisingly, it is quite important constraint - there are many more options without the restriction on colors. We'll put the check in the main algorithm later.
Generating moves
Before looking at the main part, there are two more functions we need. Given a part
(which can be Straight or Turn), current position and direction and also the current
state, we want to get all valid directions and locations for the next part:
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: |
|
Backtracking using recursion
So far, most of the code was quite easy. You can explain the type definitions to people without any technical skills. Understanding the main algorithm probably requires some programming background, but it is still surprisingly simple.
We write a recursive function solve that keeps the current position and
direction (pos and dir), the current state of the cube (set of occupied
positions) and a trace. The trace is a list of places where we put cubes
earlier and this will contain the final result at the end.
The last parameter is shape which is the list of parts. As we iterate, we
always take out the head of the list and call the function recursively for
the tail (the rest of the list excluding the first part):
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: |
|
The solve function uses pattern matching to handle three different cases:
-
The pattern
[part]checks that there is just one last part left. In that case, we have a solution - because we already checked that the position is legal. So, we just return the trace and reverse it to get the steps from the first to the last. -
The pattern
part::shapechecks that we have one or more parts and gives us the first one aspart. We also decompose the position intox,y,zso that we can check whether the color of the part matches the required color.If all conditions are satisfied, we call
getValidPositionsto get all valid positions for the next step, iterate over them and try to return all possible results usingyield!(more about this later). -
The last case represents the case when the colors do not match. In this situation, we just "do nothing" and return back to the previous step.
Note that the whole function is wrapped in the seq { .. } block. This
means that we can generate all possible solutions (we return one using
the yield keyword). In practice, it turns out that they are all symmetric, but
this was an interesting experiment :-).
Solving the puzzle
So, we finally have all we need to solve the puzzle! Now comes the tedious part, which is looking at the puzzle and noting down the exact sequence of colors and kinds. I did this by writing down two strings:
1: 2: 3: 4: 5: 6: 7: 8: 9: |
|
To my surprise, I actually wrote this down correctly at the first attempt!
Now, we just call the solve function - we need to pick the first location
and the first direction. It turns out that starting in one of the corners works
fine. In that case, the direction does not matter (because they will all be
symmetric):
1: 2: 3: 4: 5: 6: 7: 8: 9: |
|
This prints a sequence of X, Y and Z coordinates of the parts. With a bit of effort, you can actually build the puzzle using this information, because you always know where the next part should go. This is what I did at first.
But then I realized that I could do one more step and make the demo really fun!
Building 3D visualization
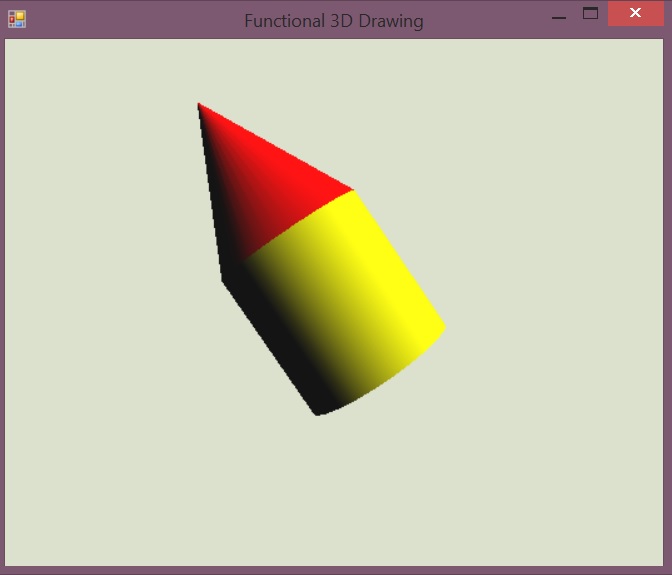
Some time ago, I wrote a simple library for composing 3D objects and it turns out to be a perfect fit. The library provides a couple of primitive shapes like cube, cone and cylinder and combinators for putting them together. Here is a simple example:
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: |
|
In just a two lines of code (if you do not try to format things nicely for a blog), you can easily put together a simple tower!
By default, all objects are created in the middle of the world, so if
we want to compose them, we have to use Fun.translate to move them
around. Then you can use the $ operator to combine multiple shapes
into a single one.
Visualizing cube puzzle
Building a visualization for the cube puzzle is quite simple. We write
a function draw i that takes the first i elements of the trace,
generates one cube for each of them and moves them to the right position:
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: |
|
The function first generates a sequence of cubes and then composes them
into a single big 3D shape using the Seq.reduce function. This applies
the $ operator gradually to all parts building the final object.
Now we can call this from a simple asynchronous loop that adds steps one-by-one, with a 200ms delay between them:
1: 2: 3: 4: |
|
The computation waits 200ms, then it builds the 3D model of the next step
and displays it using Fun.show. We start the computation using
Async.StartImmediate, which makes sure that all the processing is done
on the main user-interface thread and so we can access the UI elements and
actually update the control showing the visualization.
Conclusions
First of all, let the results speak for themselves:
I think it is quite amazing how much can be done in such a small number of lines of code in so little amount of time.
After watching people play with the puzzle for a couple of days, I wrote most of the code to solve the puzzle in about 1.5 hours during a New Year's afternoon and eve and the puzzle was solved! This alone would be quite nice, but the fact that I was able to add visualization in about 15 minutes made this really a nice example of why programming with F# is fun :-).
So, if you want to impress your family and friends with your programming skills, learning F# is most certainly the way to go!
| Black
| White
Full name: Puzzling-fsharp.Color
| Straight
| Turn
Full name: Puzzling-fsharp.Kind
Full name: Puzzling-fsharp.Part
Full name: Puzzling-fsharp.Position
val int : value:'T -> int (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.int
--------------------
type int = int32
Full name: Microsoft.FSharp.Core.int
--------------------
type int<'Measure> = int
Full name: Microsoft.FSharp.Core.int<_>
Full name: Puzzling-fsharp.Direction
Full name: Puzzling-fsharp.Shape
Full name: Microsoft.FSharp.Collections.list<_>
Full name: Puzzling-fsharp.move
Given 'Position' and 'Direction' calculate
a new position (by adding the offsets)
Full name: Puzzling-fsharp.offsets
For a 'Turn' part oriented in the given 'Direction'
generate a list of possible next Directions
Full name: Puzzling-fsharp.rotate
Given a current 'Position' and 'Direction', get a list
of possible new Directions and corresponding Positions
Full name: Puzzling-fsharp.CubeState
A set of occupied positions
module Set
from Microsoft.FSharp.Collections
--------------------
type Set<'T (requires comparison)> =
interface IComparable
interface IEnumerable
interface IEnumerable<'T>
interface ICollection<'T>
new : elements:seq<'T> -> Set<'T>
member Add : value:'T -> Set<'T>
member Contains : value:'T -> bool
override Equals : obj -> bool
member IsProperSubsetOf : otherSet:Set<'T> -> bool
member IsProperSupersetOf : otherSet:Set<'T> -> bool
...
Full name: Microsoft.FSharp.Collections.Set<_>
--------------------
new : elements:seq<'T> -> Set<'T>
Full name: Puzzling-fsharp.colorMap
Expected colors for each position
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.dict
Full name: Puzzling-fsharp.isValidPosition
Checks that the specified position is "inside" the
cube and there is no part already in that place
Full name: Microsoft.FSharp.Core.Operators.not
Full name: Puzzling-fsharp.getPositions
Given a current Position & Direction and current
Part, get a list of next Positions & Directions
Full name: Puzzling-fsharp.getValidPositions
Get next valid positions (with directions)
Full name: Puzzling-fsharp.solve
Recursive function that solves the puzzle using backtracking
val seq : sequence:seq<'T> -> seq<'T>
Full name: Microsoft.FSharp.Core.Operators.seq
--------------------
type seq<'T> = System.Collections.Generic.IEnumerable<'T>
Full name: Microsoft.FSharp.Collections.seq<_>
module List
from Microsoft.FSharp.Collections
--------------------
type List<'T> =
| ( [] )
| ( :: ) of Head: 'T * Tail: 'T list
interface IEnumerable
interface IEnumerable<'T>
member GetSlice : startIndex:int option * endIndex:int option -> 'T list
member Head : 'T
member IsEmpty : bool
member Item : index:int -> 'T with get
member Length : int
member Tail : 'T list
static member Cons : head:'T * tail:'T list -> 'T list
static member Empty : 'T list
Full name: Microsoft.FSharp.Collections.List<_>
Full name: Microsoft.FSharp.Collections.List.rev
Full name: Microsoft.FSharp.Core.Operators.fst
Full name: Microsoft.FSharp.Collections.Set.add
Full name: Puzzling-fsharp.puzzle
from Microsoft.FSharp.Collections
Full name: Microsoft.FSharp.Collections.Seq.map2
Full name: Microsoft.FSharp.Collections.List.ofSeq
Full name: Puzzling-fsharp.start
Full name: Puzzling-fsharp.res
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.set
Full name: Puzzling-fsharp.solution
Full name: Microsoft.FSharp.Collections.Seq.head
Full name: Microsoft.FSharp.Collections.Seq.iteri
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.printfn
from Functional3D
Full name: Functional3D.Fun.color
Set color to be used when drawing the specified 3D objects
struct
member A : byte
member B : byte
member Equals : obj:obj -> bool
member G : byte
member GetBrightness : unit -> float32
member GetHashCode : unit -> int
member GetHue : unit -> float32
member GetSaturation : unit -> float32
member IsEmpty : bool
member IsKnownColor : bool
...
end
Full name: System.Drawing.Color
Full name: Functional3D.Fun.cylinder
Generates a 3D cylinder object of a unit size
Full name: Functional3D.Fun.translate
Move the specified object by the provided offsets
Full name: Functional3D.Fun.cone
Generate the sphere
Generates a 3D cylinder object of a unit size
Full name: Puzzling-fsharp.fl
Convert coordinate to float values
val float : value:'T -> float (requires member op_Explicit)
Full name: Microsoft.FSharp.Core.Operators.float
--------------------
type float = System.Double
Full name: Microsoft.FSharp.Core.float
--------------------
type float<'Measure> = float
Full name: Microsoft.FSharp.Core.float<_>
Full name: Puzzling-fsharp.draw
Draw the first 'i' steps of the puzzle
Full name: Microsoft.FSharp.Collections.Seq.take
Full name: Microsoft.FSharp.Collections.Seq.map
Full name: Functional3D.Fun.cube
Creates a 3D cube of unit size using the current color
Full name: Functional3D.Fun.scale
Scale the specified 3D object by the specified scales along the 3 axes
Full name: Microsoft.FSharp.Collections.Seq.reduce
type Async
static member AsBeginEnd : computation:('Arg -> Async<'T>) -> ('Arg * AsyncCallback * obj -> IAsyncResult) * (IAsyncResult -> 'T) * (IAsyncResult -> unit)
static member AwaitEvent : event:IEvent<'Del,'T> * ?cancelAction:(unit -> unit) -> Async<'T> (requires delegate and 'Del :> Delegate)
static member AwaitIAsyncResult : iar:IAsyncResult * ?millisecondsTimeout:int -> Async<bool>
static member AwaitTask : task:Task -> Async<unit>
static member AwaitTask : task:Task<'T> -> Async<'T>
static member AwaitWaitHandle : waitHandle:WaitHandle * ?millisecondsTimeout:int -> Async<bool>
static member CancelDefaultToken : unit -> unit
static member Catch : computation:Async<'T> -> Async<Choice<'T,exn>>
static member FromBeginEnd : beginAction:(AsyncCallback * obj -> IAsyncResult) * endAction:(IAsyncResult -> 'T) * ?cancelAction:(unit -> unit) -> Async<'T>
static member FromBeginEnd : arg:'Arg1 * beginAction:('Arg1 * AsyncCallback * obj -> IAsyncResult) * endAction:(IAsyncResult -> 'T) * ?cancelAction:(unit -> unit) -> Async<'T>
static member FromBeginEnd : arg1:'Arg1 * arg2:'Arg2 * beginAction:('Arg1 * 'Arg2 * AsyncCallback * obj -> IAsyncResult) * endAction:(IAsyncResult -> 'T) * ?cancelAction:(unit -> unit) -> Async<'T>
static member FromBeginEnd : arg1:'Arg1 * arg2:'Arg2 * arg3:'Arg3 * beginAction:('Arg1 * 'Arg2 * 'Arg3 * AsyncCallback * obj -> IAsyncResult) * endAction:(IAsyncResult -> 'T) * ?cancelAction:(unit -> unit) -> Async<'T>
static member FromContinuations : callback:(('T -> unit) * (exn -> unit) * (OperationCanceledException -> unit) -> unit) -> Async<'T>
static member Ignore : computation:Async<'T> -> Async<unit>
static member OnCancel : interruption:(unit -> unit) -> Async<IDisposable>
static member Parallel : computations:seq<Async<'T>> -> Async<'T []>
static member RunSynchronously : computation:Async<'T> * ?timeout:int * ?cancellationToken:CancellationToken -> 'T
static member Sleep : millisecondsDueTime:int -> Async<unit>
static member Start : computation:Async<unit> * ?cancellationToken:CancellationToken -> unit
static member StartAsTask : computation:Async<'T> * ?taskCreationOptions:TaskCreationOptions * ?cancellationToken:CancellationToken -> Task<'T>
static member StartChild : computation:Async<'T> * ?millisecondsTimeout:int -> Async<Async<'T>>
static member StartChildAsTask : computation:Async<'T> * ?taskCreationOptions:TaskCreationOptions -> Async<Task<'T>>
static member StartImmediate : computation:Async<unit> * ?cancellationToken:CancellationToken -> unit
static member StartWithContinuations : computation:Async<'T> * continuation:('T -> unit) * exceptionContinuation:(exn -> unit) * cancellationContinuation:(OperationCanceledException -> unit) * ?cancellationToken:CancellationToken -> unit
static member SwitchToContext : syncContext:SynchronizationContext -> Async<unit>
static member SwitchToNewThread : unit -> Async<unit>
static member SwitchToThreadPool : unit -> Async<unit>
static member TryCancelled : computation:Async<'T> * compensation:(OperationCanceledException -> unit) -> Async<'T>
static member CancellationToken : Async<CancellationToken>
static member DefaultCancellationToken : CancellationToken
Full name: Microsoft.FSharp.Control.Async
--------------------
type Async<'T>
Full name: Microsoft.FSharp.Control.Async<_>
Full name: Microsoft.FSharp.Core.ExtraTopLevelOperators.async
Full name: Functional3D.Fun.show
Display the specified 3D object on a form
Published: Tuesday, 25 March 2014, 3:27 PM
Author: Tomas Petricek
Typos: Send me a pull request!
Tags: f#, fun, functional programming