Accelerator and F# (II.): The Game of Life on GPU
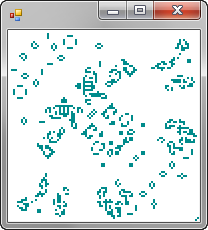
In the previous article, I introduced the Microsoft Research Accelerator library. It allows us to write computations with arrays in C# and execute them in parallel on multi-core CPU or more interestingly, using GPU shaders. In the previous artcile, we've seen how Accelerator works and how it can be accessed from F#. In this article, we'll look at one more interesting F# demo - we'll implement the famous Conway's Game of Life [1] using Accelerator. We'll use a v2 version of Accelerator which has been announced just recently and is available from Microsoft Connect [2].
This article is the second one from a series about using Accelerator from F#. Today, we'll use Accelerator types directly from F# - this is the simplest possible approach and is very similar to the way you'd work with Accelerator in C#. However, we can use some nice F# features such as custom operators to make the code more readable. In the next article, we'll discuss a different approach - we'll look how to execute more "standard" F# code (that doesn't reference Accelerator explicitly) with Accelerator using F# quotations. The list of articles may change, but here is a list of articles that I'm currently planning to write:
- Accelerator and F# (I.): Introduction and calculating PI
- Accelerator and F# (II.): The Game of Life on GPU
- Accelerator and F# (III.): Data-parallel programs using F# quotations
- Accelerator and F# (IV.): Composing computations with quotations
Implementing the Game of Life
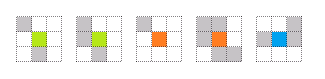
The Game of Life is a zero-player game, which means that once we start it with some initial configuration, it will run without any other input. It runs on a square grid and looks like a cell or simple organism simulation. In each step, some of the organisms die and some new organisms appear, so we'll just need to calculate a new state of the grid. The game is truly amazing, because it has extremely simple set of rules, but can create fantastic and very complicated structures. In fact, it is Turing-complete, which (roughly) means that you could encode arbitrary computer program with its inputs as an initial configuration of the Game of Life and it would simulate the program. It would require some additional coding of inputs and outputs as well as an extremely large grid, but it is theoretically possible!
You can see the rules of the game visualized in the diagram above:
- Green - When an existing cell (green in the middle) has three or two neighbours it survives to the next round
- Red - When an existing cell has less than two neigbors it dies, because it is lonely (first red case), when it has more than three neighbors it dies of overcrowding (second red case)
- Blue - Finally, a new cell is born in an empty grid location if there are exactly three neighbors.
As you can see, there are only three simple rules that drive the Game. Our implementation will simply need to calculate a new state of the grid based on the original one and for each element of the array, we'll check the three rules. However, before looking at the implementation, we'll write a couple of constants to configure the game and a few hlepers.
Getting ready
Our implementation allows us to specify the size of the grid (it has to be a square)
and a size of the window. The visualization looks the best when the size of the
window is a multiple of the grid size. Once we know the size, we'll initialize
a couple of FloatParallelArray instances representing arrays
of the specified size that contain constant values. We're using the FPA
type alias from the previous article.
// Configuration of the game
let gridSize, formSize = 512, 512
// Initialization of constant 2D arrays
let shape = [| gridSize; gridSize; |]
let [zero; one; two; three] =
[ for f in [0.0f; 1.0f; 2.0f; 3.0f] -> new FPA(f, shape) ]
The code uses a simple sequence expression that iterates over a list of
constants stored as floats and yields a new FPA instance with
the required size. Note that we're using a compact syntax of sequence
expressions, because we only need to perfrom a projection. The result
of the sequence expression is a list and we use pattern matching to
decompose the list into individual elements. The compiler cannot verify
at compile-time that the number of elements will match, so it will issue
a warning. However, we know that the code is correct in this case, so we don't
need to worry. You can also turn the warning off by adding #nowarn "25"
to the beginning of the file.
Now that we know the size of the grid and have all the needed constant arrays, we'll also implement a single function that wrap the Accelerator functionality and three custom operators:
// Calculating with 2D float arrays
let rotate (a:FPA) (dx:int) dy = PA.Rotate(a, [| dx; dy |]);
// Custom operators - simulating logical operations using floats
let (&&.) (a:FPA) (b:FPA) = PA.Min(a, b)
let (||.) (a:FPA) (b:FPA) = PA.Max(a, b)
let (==.) (a:FPA) (b:FPA) = PA.Cond(PA.CompareEqual(a, b), one, zero)
As you can see, all of our functions and operators are simple wrappers for
static methods of the ParallelArrays class (type alias PA).
This makes the F# code more idiomatic and also allows us to use operators
with the infix notation. The names of the operators ends with an additional
dot to denote that they implement point-wise operations.
The rotate function moves elements of the array by the specified
offset (it is a bit similar to Shift that we discussed in the
previous article). However, when elements
is shifted outside outside of the grid, values are copied back from
the other side. To demonstrate this, if we moved the contents of 1D array
[1; 2; 3; 4; 5] by +2, we'd get [4; 5; 1; 2; 3].
Next, we define three operators that simulate Boolean operations
using floats. Accelerator also provides BoolParallelArray type,
which can be used for calculating with arrays of Booleans, but we'll need
to combine calculations with floats and Booleans in more sophisticated ways,
so simulating logical operations with floating point numbers works better.
- The
&&.operator simulates and by returning the minimum of the two values. This means, that the result will be 1 only if both of the inputs contain 1. If any of the inputs contains 0, the overall result will be 0. - The
||.operator simulates logical or using maximum. This means that the result will be 1 if any of the inputs contains 1. - Finally, the
==.operator implements an equality check usingCompareWithandCond. When the values are equal, it returns a value fromoneand otherwise it returns a value fromzero.
Now we can manipulate with the game grid using rotate and also
simulate logical operations using floating point values 1.0 and 0.0. Let's
finally look how we could implement a single step of the Game of Life.
Calculating the game step
The state of the game will be represented as a 2D array float32[,].
We'll need some interesting initial state for the game, so we'll set all values
to zero with the exception of a diagonal from left-upper location (when x = y)
and the first row and column of the grid (x = 0 || y = 0). This is
enough to start a very interesting simulation. If you'll later want to experiment
with the code, you may try changing the initial configuration:
// Create an initial data grid
let initial = Array2D.init gridSize gridSize (fun x y ->
if x = 0 || y = 0 || x = y then 1.0f else 0.0f)
The code uses F# library function Array2D.init, which takes the
dimensions of an array as first two arguments. The last argument is a function
that calculates a value of the array at the specified coordinate. Otherwise, the
listing doesn't show anything interesting. The function that calculates the
next state of the grid is much more interesting. We'll start by writing a function
that takes FPA as an input and returns FPA as the
result. As I explained earlier, this is just a representation of a computation
that can be executed later. We'll run the constructed computation later to get a
result of type float32[,], which can be easily visualized.
let nextGeneration (grid:FPA) =
// Generate grids shifted by 1 in every direction
let hd::tl =
[ for dx in -1 .. 1 do
for dy in -1 .. 1 do
if dx <> 0 || dy <> 0 then
yield rotate grid dx dy ]
// Count neighbors of each grid element
let sum = tl |> List.fold (+) hd
// Implements the Game of Life logic
(sum ==. three) ||. ((sum ==. two) &&. grid)
In the first step, the function creates a list of 8 grids rotated in all
of the 8 possible directions (north, northeast, east, southeast, etc).
This is implemented as a sequence exprssion that generates a single rotated
grid for each combination of offsets (dx and dy).
It only skips the combination when both dx and dy
are zero (which would correspond to the original grid). Note
that we decompose the created list into a head (first element) and a tail
(list of all remaining elements), because this will make further processing
easier.
Now we have 8 grids, which represent the original grid shifted in each
direction. If we put all these layers over each other and count the number
of living cells in each location, we'll get the number of neighbors for
each location. This is exactly what the next line does. We're using the
List.fold function with the first grid (hd) as an initial value and
the overloaded point-wise addition of arrays (+ for the FPA
type) as the aggregation function. By running the aggregation with the remaining
7 grids (tl) as the source specified using pipelining, we'll get
the count of neighbors.
Finally, the last line implements the Game of Life logic using our custom logical operators. We use a slightly different (but equivalent) encoding of the original three rules - a specific location in the newly constructed grid will contain a living cell if and only if it originally had three living cells as neighbors (in this case we don't care whether there was originally a living cell in this location) or if there was a living cell originally and had two neighbors.
Without any doubt, the last line of our code makes the F# implementation of the Game of Life using Accelerator really neat. A single succinct line of code impplements all the game logic. Now we only need to add some code to visualize the Game, so that we can see the complex behavior patterns it creates...
Visualizing the game
To actually run the computation and display the results, we'll need to specify
the target, which is an Accelerator engine, which we can use to evaluate
FPA computations. We'll implement the game as a function that
takes the target as an arguments, implements two local functions and then
instantiates the DrawingForm type. This is a form that keeps
running the step operation in a loop and we'll look at its source in
the next subsection.
let life(target:Target) =
// Functions to calculate next state and to draw it
let nextState (g:float32[,]) =
target.ToArray2D(nextGeneration(new FPA(g)))
let display (data:float32[,]) =
data |> toBitmap (fun f ->
if (f < 0.5f) then Color.White else Color.DarkCyan)
// Run the drawing form with life game
let gameForm =
new DrawingForm<_>
(initial, nextState, display,
ClientSize = Size(formSize, formSize))
Application.Run(gameForm)
do
life(new DX9Target())
We already have the nextGeneration function, which has a type
FPA -> FPA. It returns a computation that represents the next
step of the game. As we said earlier, we'll keep the current state as a type
float32[,] that contains actual grid values instead of some
abstract computation. The function nextState calculates the
new state using the final representation. It takes an array as an argument,
wraps it into FPA type, then calculates the next generation and
evaluates the result using the specified target. The type of this function
is float32[,] -> float32[,].
The second local function is display. It is used to visualize
the current state in a bitmap. This function has a type float32[,] -> Bitmap.
We implement it using a higher-order function toBitmap which takes
a 2D array as an argument and a function that turns a value from the array
(in our case float32) into a pixel color. We provide a simple function
that returns white color for values 0.0 and dark cyan for values 1.0. The toBitmap
function isn't a part of standard F# libraries - it is implemented using direct
memory access, which is unsafe, but efficient. You can find the implementation
in the source code at the end of the article.
The last part of the function initializes the DrawingForm type.
This is a reusable type that we'll implement shortly. It can be used for running
any simulations where we want to calculate new state as fast as possible
and redraw the form after every recalculation. We give it three parameters -
an initial state, a function to calculate new state and a function that draws
the current state into a bitmap. Note that the state is a generic type parameter.
We don't need to know what the state is as long as we're able to create a bitmap
from it. The last step we need to do is to implement the DrawingForm type...
Implementing a drawing form
The DrawingForm type is a generic class with a single type parameter
and three constructor parameters. The type parameter represents a state, which is
recomputed using the provided function when the form is running. We'll implement
the form using the implicit class syntax:
type DrawingForm<'TState>(initial, update, draw) as x =
inherit Form()
// Loop that runs computation & redraws form
let rec drawingLoop(state) =
if not x.IsDisposed then
( use gr = x.CreateGraphics()
gr.InterpolationMode <- Drawing2D.InterpolationMode.NearestNeighbor
gr.DrawImage(draw(state), x.ClientRectangle) )
drawingLoop(update(state))
do
// Run the computation
Async.Start(async { drawingLoop(initial) })
The form doesn't contain any members, so the entire body is essentially just a
constructor. The constructor parameters (an initial state and two functions) are
written directly following the type name. It starts by inheriting from the .NET
Form type. Next, it declares a single local recursive function
drawingLoop the function runs until the form is closed. It keeps the
current state as a parameter (which is a typical functional technique).
After making sure that the form is still displayed, it redraws the graphics
using the current state. Note that we use the use keyword to dispose
the gr object when it is no longer in scope. In this case, we
need to specify the scope explicitly using parentheses.
Inside the drawing code, we need to obtain a bitmap to draw on the form. We
do it by calling the draw function (a constructor parameter) with
the current state as an argument. Once we're done with drawing, we calculate
new state by calling the update function and continue looping
by recursively invoking drawingLoop.
Finally, the do block contains code that's executed when the object is created.
The only thing we do is that we start the function performing the drawing on
a background thread. Note that this is safe, because CreateGraphics
method is one of the few members of the Form type that can be
accessed from non-GUI threads. We use a single asynchronous workflow to
start the computation. This is simply a convenient way to start a background
task, because Async.Start starts executing the workflow in
background.
Extending the example
And that's it! There are various ways to make the application more interesting. One option is to enable some user interaction. The source code below adds a simple handler for mouse click. When you click on the form using left button, it will add some randomly located living cells and right button removes some of them. This allows you to create some nice patterns:
Summary
In this article, we've seen an interesting demo of using the Accelerator library
from F#. We've used many of the standard methods for working with FloatParallelArray
type, which is the core of Accelerator. Among others, we've used Rotate for calculating
neighbors and Min, Max together with Cond to implement
logical operators for working with arrays. Then we encoded the logic of the Game of Life using
a simple data-parallel expression that allows the Accelerator to run the code efficiently in parallel
either using GPU or using multi-core CPU.
There are still many interesting things to explore. We've already seen two examples of using Accelerator from F# in the direct way, so we won't look at more complicated demos. Instead, we'll look at more sophisticated way of using Accelerator. In the next part, we'll use F# quotations (which are similar to C# expression trees) to write the data processing code as a standard F# code (this for example enables easier debugging) and then execute it using Accelerator.
Downloads and References
- Download the Game of Life (ZIP, 5.5kB)
- Download video (WMV, 2.35MB)
- [1] Conway's Game of Life - Wikipedia.org
- [2] Microsoft Research Accelerator v2 - Microsoft Connect
- [3] GPGPU and x64 Multicore Programming with Accelerator from F# - Satnam Singh's blog at MSDN
Published: Monday, 28 December 2009, 9:16 PM
Author: Tomas Petricek
Typos: Send me a pull request!
Tags: academic, functional, meta-programming, accelerator, f#, math and numerics