Accelerator and F# (IV.): Composing computations with quotations

In this article series, we're talking about the Accelerator project and I'm
presenting an F# library that I implemented, which allows you to use Accelerator [references]
in a more sophisticated way. We've seen two examples of using Accelerator directly
(see also introduction and Game of Life).
In the previous article
I introduced my F# library for working with Accelerator. We've seen F# functions from the
DataParallel module, we implemented an algorithm that rotates an image
using these functions and finally, we've seen that we can take this ordinary F# code
and run it using Accelerator. This is all possible thanks to F# quotations, which
we can use to get an AST (a source code) of an F# function we wrote (if the function
is marked in some special way).
In this part of the series, we're going to look at working with quotations explicitly. We'll use meta-programming techniques to work with Accelerator. Meta-programming means writing programs that manipulate with other programs or pieces of code. This is exactly what we're going to do in this article. We'll write an F# function (running on CPU) that builds a program, which we'll then run using Accelerator.
This is quite interesting approach, which isn't possible when we call Accelerator methods as standard F# functions or .NET methods. The benefit is that we'll clearly see which parts of program run on CPU and what parts execute on GPU or using X64 multi-core target. We could also perform more complicated optimizations with the code (because this wouldn't affect the readability). Just for your reference, here is the list of articles in this series in case you missed some of them:
- Accelerator and F# (I.): Introduction and calculating PI
- Accelerator and F# (II.): The Game of Life on GPU
- Accelerator and F# (III.): Data-parallel programs using F# quotations
- Accelerator and F# (IV.): Composing computations with quotations
However, enough with theory and let's take a look at some code samples! This time, we'll implement blurring of an image (also called convolution). Another example how to write this in F# using Accelerator is Satnam Singh's blog post [4]. Our example will be different, because we'll write the code as standard F# program and then have it translated to Accelerator automatically using quotations. We'll also talk about the architecture of the library that we're using and look at some performance results.
Blurring an image
To blur an image, we'll shift the image in both X and Y directions with
some specified offsets. This way, we'll get a multiple copies of the same
image shifted in various directions. We'll calculate weighted average of
all the images. This means that the bigger the offset will be, the less
importance we'll give to the copy. We'll start by referencing several
namespaces, including F# Math namespace from PowerPack.dll
and Quotations namespace for working with F# quotations.
We also reference several namespaces from my library for translating
data-parallel F# code to Accelerator code.
// Reference F# libraries
open Microsoft.FSharp.Math
open Microsoft.FSharp.Quotations
module Matrix = Math.Matrix.Generic
// Quotations translator & float4
open FSharp.Math
open FSharp.Accelerator
Now that we have the references, we can start implementing the actual blur. We'll start by calculating a kernel, which is an array with coefficients that we'll use when composing shifted images.
Calculating kernel
We'll use an algorithm that's based on a sample that ships with Accelerator and is called Gaussian filter. This means that for an offset j, the value in the kernel will be exp(j2 / 2σ2) for some constant σ. Then we'll also normalize the kernel, to make sure that the values add up to 1.
// Compute kernel for the blur algorithm
let computeCoefficients size =
let halfSize = size / 2
let gauss = List.init size (fun i ->
Math.Exp(-float((i - halfSize) * (i - halfSize)) / 8.0))
// Normalize values and convert them to 'float4'
let sum = List.sum gauss
[ for v in ia -> Float4.ofSingle(float32(v / sum)) ]
Inside the body of the function, we first initialize a list with
values of the Gaussian function using List.init. To normalize
the values, we simply sum all values using List.sum and then
divide each element of the kernel by the sum. This is written using a simple
list-comprehension. Note that we also convert the result to a value of
float4 type, because we'll use it with a type representing
an image (just like in the previous article, this type will be
Matrix<float4>).
Variables inside quotations
First of all, we'll need one more utility function. The makeBlurImage
function will construct an expression that represents F# code, which performs
blurring of an image. We'll need to use a few variables inside the generated
expression. To create variables inside generated F# quotation, we'll use the
following utility:
let variable<'TResult> name =
let var = Var.Global(name, typeof<'TResult>)
let expr = Expr.Cast<'TResult>(Expr.Var(var))
var, expr
This function creates a new variable of type 'TResult with a
name name. It returns a tuple Var * Expr<'TResult>.
The first element of a tuple is an object that represents the variable.
The second element is a typed F# quotation that represents code that reads
the value of the variable. The quotation is typed, which means that it
carries the type of the expression as a type parameter. In this case, the
type of the expression is obviously the same as the type of the variable
('TResult).
Implementing the blur filter
Now that we have a utility function for working with variables inside
quotations, let's look at the makeBlurImage function. The implementation
requires more explanation, so we'll split it between three listings.
We'll look only at the body, because the declaration is quite simple.
The function takes only a single parameter named kernel,
which is a list of float4 values representing coefficients
used for blurring. Now, let's take a look at the first part of the function:
// Compute kernel with offsets
let half = kernel.Length / 2
let indices = [-half .. kernel.Length-half-1]
let kernel = List.zip kernel indices
// Parameter of the returned function
let inputVar, inputExpr = variable<Matrix<float4>> "input"
We start by adding zipping the kernel with indices that represent
offset used when shifting the image. For example, if we received a
kernel containing 3 values such as [0.2; 0.6; 0.2], we'd
join it with indices [-1; 0; 1]. The result would be
[(0.2, -1); (0.6, 0); (0.2, 1)]. We'll use this list
shortly. We'll create a multiple copies of the image, shift it by
the offset specified as the second element of the tuple and multiply it by
the value specified as the first element to get a couple of images that
add up to a single blurred image.
The last line of the code creates a variable named input.
We'll use it as an input parameter of a quoted function that we'll construct.
You can imagine as if we were writing something like <@@ fun input -> ... @@>.
Now, let's take a look at the code that generates the ...
part of the expression.
// Compose convolution in X direction
let initial = <@@ zerof4 (%inputExpr).Dimensions @@>
let convolvedX =
kernel |> List.fold (fun st (v, idx) ->
<@@ (%st) .+ (shift (%inputExpr) 0 idx) *| v @@>) initial
This bit of code is far more interesting. It starts by declaring a
value initial. The initialization expression is a quotation
that calls the zerof4 function to initialize a matrix filled
with zeros. The function takes dimensions as an argument and we give it
dimensions of the input matrix as the argument. We invoke the Dimensions
property on an expression (%inputExpr). This construct is
called a splice and it means that we're embedding another quotation
inside the quotation we're currently writing. We created inputExpr
earlier as a quotation that represents reading of the input variable. Here,
we splice it into a larger quotation that gets a property of this variable and
then uses the result as an argument of some function.
The idea of splicing is very important and we'll need it a couple of times
in this article, so let me show you one more example. Let's say we declared
a value added = <@@ 2 + 3 @@>. Now, we can use the
splicing operator % to insert the quotation into another, larger
quotation: <@@ (%added) * (%added) >. If you now examine the
result, you'll see that we created a quotation <@@ (2+3) * (2+3) @@>.
Once we have the initial value representing an empty image,
we use the fold function to construct more complicated quotation
based on the kernel value. In each step, we create a quotation that
takes the previous one (%st) and adds it with a value calculated
by (shift (%inputExpr) 0 idx) *| v. This represents the input
image (%inputExpr) shifted by idx in the second coordinate
and finally, multiplied by the coefficient v, which comes
from the kernel. If we evaluated the function so far and looked at the generated
quotation, the result would look like this (except, we didn't yet join
the body with the parameter declaration into a function):
fun input ->
(zerof4 input.Dimensions) .+ ((shift input 0 -1) *| 0.2f) .+
((shift input 0 0) *| 0.6f) .+ ((shift input 0 1) *| 0.2f)
As you can see, we've just performed a convolution by the second coordinate.
Now, we'll do a very similar thing using the first coordinate. Instead of
just blindly replicating the above displayed generated code 3 times, we'll
store the result in a new variable named convolvedX and
then blur this partially blurred image by the second coordinate.
// Store the convolved result in a variable
let convXVar, convXExpr = variable<Matrix<float4>> "convolvedX"
// Compose convolution in Y direction
let body = kernel |> List.fold (fun st (v, idy) ->
<@@ (%st) .+ (shift (%convXExpr) idy 0) *| v @@>) initial
let convXDecl = Expr.Let(convXVar, convolvedX, body)
Expr.Lambda(inputVar, convXDecl)
We start by declaring a new variable named convolvedX which we'll
use to store the result of the computation we wrote so far. The middle part of the
listing is very similar to the previous one. We again generate a quotation that
adds the initial (empty) image with a series of images shifted by a specific offset
and multiplied by a value specified by the kernel. Note that the image we use as
a parameter to the shift function is the one stored in the convolvedX
variable, because the argument of the splicing operator is an expression that represents
reading of its value (%convXExpr).
Finally, in the last two lines, we create a quotation that joins everything we wrote
so far together. The first line declares a value binding that declares the
convolvedX variable and the second line builds a lambda function that we
return as the result. The generated quotation looks like this: (fun input ->
let convolvedX = comp1 in comp2). The
first placeholder represents a computation that we constructed in the preceding
listing and the second placeholder represents the code we constructed now.
Composing data-parallel code using F# quotations as we've seen in this section isn't easy to understand if you're not already familiar with meta-programming techniques. The important point that you need to realize is that we're writing code that constructs some other code. In our case, we're writing code that runs on CPU and that constructs data-parallel program, which will run using Accelerator. However, the nice thing about this approach is that you can clearly see which part of the code runs now (e.g. both of the folds) and which will run later (shifting and point-wise addition of matrices inside the quoted code).
Running blur filter
We now have a function that builds a quoted code that implements the blur filter
and can be translated to Accelerator calls. The last step is to run the function
and give the resulting code to a library that actually performs the blur (we'll
use the DX9Target, which will perform the data-parallel operations
on GPU).
do
let target = new Microsoft.ParallelArrays.DX9Target()
let bmp = Bitmap.FromFile(Application.StartupPath+"\\prague.jpg") :?> Bitmap
|> Conversions.matrixOfBitmap Float4.ofColor
let coefs = computeCoefficients 10
// Accelerated version of blur
let accelerated = Accelerate.accelerate (makeBlurImage coefs)
let run data =
eval<Matrix<float4>>
target accelerated [ makeValue data ]
DrawingForm.Run(bmp, run, Conversions.bitmapOfMatrix Float4.toColor)
The listing first initializes Accelerator target and then loads a bitmap
from the startup path of the application. We immediately convert the bitmap to
a type Matrix<float4>, which we'll use as an input to our
data-parallel blur. Once we have the input, we construct a function
run, which takes a bitmap (represented as a matrix), blurs it and
returns the result (again, as a matrix). To do this, we first invoke
makeBlurImage with a kernel as an argument. The result of this call
is a quotation of a function performing the blur filter. We pass the quotation
to the accelerate function, which analyzes it and gives us a function
which performs the data-parallel blur using Accelerator.
Inside the run function, we use eval to invoke the
accelerated function. We give it a target to use for evaluating data-parallel
operations and we wrap the single argument into a TransformValue using
the makeValue function (as described in the previous article). As the last step, we run the application
using the DrawingForm object. It takes the initial state as the first
argument, a function that calculates the next state as the second argument and
a function that converts the state (a matrix) into a bitmap as the last argument.
Architecture & Performance
Before we conclude, let's take a look at the overall architecture of the application we just implemented (including the components from Accelerator and components from my F# library for using Accelerator). I also made some measurements, so we'll take a look at some performance results.
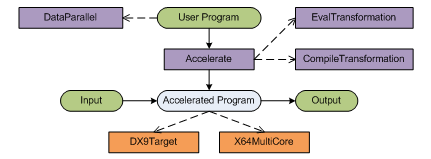
Understanding architecture
You can see a diagram showing the architecture on the right. The dashed arrows
represent references or uses of some other component. For example, the user program
we generated uses operations from the DataParallel module.
Solid arrows represent some data-flow. For example, the User Program is passed
as an input to the Accelerate component, which produces an
Accelerated Program as the result.
There are several components, so let me start by discussing them one-by-one. The violet components come from my F# library (if you download the source code, you'll see it as FSharp.Math.Accelerator.dll). The orange boxes represent components from Microsoft Research Accelerator library. Let's start by discussing the violet boxes:
- DataParallel contains operations for working with matrices
that can be easily translated to Accelerator calls (such as the
shiftfunction and the+.operator). We discussed more functions from this module in the previous article. - Accelerate implements an analysis of quoted F# programs that
implement algorithms using functions from the
DataParallelmodule. During the analysis, it composes an accelerated program (which performs the same operation using Accelerator) as the result. To compose the program, it can use one of two modules that provide slightly different behavior (EvalTransformationorCompileTransformation). - EvalTransformation evaluates the program during analysis of F# quotations (after it receives input data). This means that the analysis of quotations is done once for each call to the Accelerated Program. This is less efficient, but it makes debugging easier.
- CompileTransformation is more efficient. It analyzes quotations only once and builds a function as the result. This means that when we later run the Accelerated Program, it doesn't need to analyze quotations again. It immediately runs the algorithm we implemented using Accelerator.
Once we get the Accelerated Program using the Accelerate.accelerate function,
we need to give it some input data as an argument and it produces some output. Depending
on the Transformation component we used, this may or may not need to analyze F# quotations
internally. However, that's not visible from the outside. Aside from the input data,
we also need to specify which Accelerator target should be used when
evaluating the program. This can be one of the orange boxes:
- DX9Target performs data-parallel operations using shaders on your GPU. This is massively parallel, however there are some initial costs associated with copying data to the GPU memory and back.
- X64MultiCore performs data-parallel operations using multi-core 64bit CPU. This is using highly optimized native implementation.
If you want to use the library to run your computations with the F#
Matrix type more efficiently, you'll always use the CompileTransform
(this is specified using a compilation symbol in the downloadable source code
and it is turned on by default). Then you can choose either GPU or multi-core execution
depending on your machine.
Measuring the performance
I did some experiments on my dual-core (Intel Core 2 Duo P8400, 2.26GHz) laptop with an integrated graphics card (Intel GMA 4500MHD), so let's look at the results. Because I'm using only an integrated GPU, the numbers are better for the native multi-core implementation, but I suspect that a better GPU would give more interesting results (please drop me a note in the comments with your results if you get some interesting numbers!)
| Sample | F# matrix | Preprocessing | X64Multicore | DX9Target | Max. speedup |
|---|---|---|---|---|---|
| Life | 290ms | ~1000ms | 40ms | 130ms | 7.3x |
| Blur | 3690ms | ~2000ms | 100ms | 190ms | 36.9x |
| Pi | 1590ms | ~850ms | 490ms | 560ms | 3.2x |
| Rotate | 1250ms | ~1490ms | N/A | 220ms | 5.7x |
Even though I run the tests on a usual laptop, some of the results are
quite impressive! I implemented all the tests that we've seen in the article series so far,
so we have a Pi calculation using Monte-Carlo method, Conway's Game of Life and two
graphical filters (rotation and blur). For some reason, the rotation doesn't work when
executed with the X64MultiCoreTarget (I suspect this is a bug in the current
version of Accelerator). The most significant performance improvement can be seen in the
Blur filter, which runs almost 40 times faster compared to the naive code using F# Matrix.
I run the tests using CompileTransformation, so each test spent some
time while pre-processing the F# quotations and building the accelerated function that
we use later. This is needed only once and can be performed in advance, so it isn't a
problem in practice. You can see these times in the Preprocessing column.
Summary
In this series, we talked about the MSR Accelerator project and how to use it from F#. In the first two articles, we used it directly. This way, we work with special types provided by the Accelerator library and we write computations using methods that these types offer. This is quite easy, but we have to use different types and we can't debug the code easily (because everything runs at the end of the algorithm using GPU).
In the previous and this article, I introduced a library that I created (originally,
during an internship at MSR about two and a half years ago)! Since then, both F# and
Accelerator become available in a new version, so I updated the library using the latest
technologies. As we've seen, the library allows you to write code using the standard
F# Matrix type and then translates it automatically (using F# quotations)
to function that runs more efficiently using Accelerator. In the previous article,
we've seen that we can write data-parallel functions as normal functions and mark
them using the ReflectedDefinition attribute.
In this article, we've seen a more sophisticated technique. We used meta-programming
techniques to write a function (running on CPU) that produces a quoted function
(which can be executed using Accelerator). This way, you could easily see which part
of the code runs when, which is not easy when using Accelerator directly. In the end,
we also looked at some performance results that compare a naive code written using
Matrix type with a version optimized using the library I described.
For now, this is the last article of the series, but please let me know if there is something you'd be interested in more details! In the future, I'd also like to implement one more extension to this library, which would allow you to write the matrix processing code in a more readable way then when using data-parallel functions explicitly, so if you liked the series, stay tuned for more articles!
Downloads and References
- Download the source code (ZIP, 666kB)
- [1] Accelerator: Using Data Parallelism to Program GPUs for General-Purpose Uses - Microsoft Research
- [2] Accelerator Project Homepage - Microsoft Research
- [3] Microsoft Research Accelerator v2 - Microsoft Connect
- [4] GPGPU and x64 Multicore Programming with Accelerator from F# - Satnam Singh's blog at MSDN
Published: Tuesday, 12 January 2010, 3:20 AM
Author: Tomas Petricek
Typos: Send me a pull request!
Tags: functional, academic, meta-programming, accelerator, f#, math and numerics