Functional Programming in .NET using C# and F# (Manning Greenpaper)

Real-World Functional Programming in .NET

Functional programming languages have been around for a while and were always astonishing for their ability to express the ideas in a succinct, declarative way allowing the developer to focus on the essence of problem rather than on technical details of the solution. Recently, functional paradigm is gaining new prominence as an efficient way to handle development of multi-processor, parallel and asynchronous applications.

Available via MEAP | 500 pages
Softbound print: March 2009 (est.)

Functional ideas are arising in C# as well as in other main-stream languages and functional languages are becoming an alternative for real-world projects. Also, Microsoft recently introduced a new language called F#, which has a strong background in traditional functional languages, but as a .NET language also benefits from the rich .NET and Visual Studio ecosystem.

This article is partially an excerpt from my book Real-world Functional Programming in .NET [1]. Thanks to my editors at Manning I have the permission to publish it on my blog. We’ll look at several aspects of functional programming and how the same concepts, which are essential for the functional paradigm, look in the F# and in C# 3.0 with LINQ. We will shortly look at the basic programming language features like lambda functions and type inference that are now available in both F# and C#. Functional programming isn’t only about language features, but also about using different programming style, so we’ll look at some high level concepts as well. These include using immutable data structures for developing code that can be executed in parallel and writing code in a more declarative style.

Thanks to the combination of C# 3.0 and F#, this article shows the ideas in a way that should be familiar to you in C#, but also shows a further step that you can take with a primarilly functional language F#. If you're a .NET developer and you want to understand what functional programming is and how it can help you to become better and more productive then continue reading. If you'll find this article interesting, then don't forget to check out the book, which explains everything in larger detail and discusses many other interesting ideas.

Introduction

Functional programming differs from the usual imperative and object oriented style in many ways, so I’d like to start this article with an introduction of the basic concepts that are essential for functional programming. There are many different functional languages and every language puts emphasis on a slightly different set of concepts, but the ideas presented in section 1 are shared by almost all functional languages.

After introducing the core concepts, we’ll look at the F# language in the section 2. F# existed for a several years as a project developed and maintained by Don Syme at Microsoft Research. Recently, Microsoft announced that F# is being productized, so it is now joining the family of Visual Studio languages. F# isn’t purely functional language, but instead mixes the best from many styles, including functional and object-oriented. It is also a .NET language, so we’ll look how to use .NET libraries (like Windows Forms) from F#. As already mentioned, features typical for functional languages are now available in many non-functional languages like C# 3.0, Visual Basic and Python. We’ll look at three examples showing how the same idea looks in a primarily functional F# language and in C# in section 4.

In particular we’ll look at the list type known from many functional languages and how it relates to the iterators and the IEnumerable type in C# 2.0. Next, we’ll look at lambda functions, which is arguably the most essential feature of functional languages. Lambda functions are one of the additions to C# in the 3.0 version. The next feature that we’ll look at is generics and type inference. The development of generics for C# and .NET 2.0 was largely influenced by F#, so we’ll see how generics are important for F#. Type inference, which simplifies declaration of variables in C# 3.0, is also rooted in functional programming. The succinctness of the F# programming style is possible only thanks to the use of type inference, but thanks to the combination with generics we can get the usual safety of statically typed languages.

Next, we’ll focus our attention to topics that are very important nowadays and we’ll discuss parallel and asynchronous programming. Parallel execution means that two pieces of code execute at the same time (for example on a multi-core processor). As we’ll see functional programs avoid using global mutable state, which eliminates the common source of problems and makes writing parallel programs easier. Asynchronous programming refers to something different – when writing program that performs I/O operations or accesses web services, we often want to start executing some operation and wait until it finishes (e.g. web request), but writing this using methods like BeginInvoke is difficult, so we’ll look at the F# solution in section 4.

Finally, in the last section of this article, we’ll discuss a different point of view at programs that can be used when writing code and which is very useful when thinking about functional programs. We’ll see that library can be viewed as a language that specifies how we can some particular type of problems. We’ll shortly get back to lists and look at the library for working with lists and I’ll demonstrate an example from a more complex solution for developing animations in a functional way.

1  The elements of functional style

1.1  Values instead of variables

First of all, functional programs don’t usually have typical variables that are used for storing a state of some operation, by reading and writing a value of the variable after executing a single operation. Variables in functional languages are instead immutable, meaning that the value of variable can’t change after it has been initialized. This is a reason why functional languages usually use the term “value” instead of “variable”.

Let me demonstrate what I mean using an example. Let’s say we want to write a program that takes 0 as an initial value, reads two numbers from the console, adds the first number to the initial value and multiplies the result by the second number. A typical implementation of something like this in C# would look like this:

int res = 0;
res = res + ReadInt32();
res = res * ReadInt32();
WriteInt32(res);

As you can see, we created a variable res and modified it two times when reading the input value from the console. Now, let’s look at the same code implemented without modifying a value of variables:

int res0 = 0;
int res1 = res0 + ReadInt32();
int res2 = res1 * ReadInt32();
WriteInt32(res2);

Because we didn’t want to modify the value of existing variable we declared a new variable (res0, res1, res2) every time we wanted to calculate a new value. The key difference is that in the second example, we didn’t use the assignment operator (written as an equal sign in C#). The only occurrence of this symbol in a second example is when initializing a variable value, which has a different meaning then assignment operator – instead of changing a value of an existing variable it creates a new variable with a specified initial value.

1.2  Programming using recursion

You can probably imagine how to write some extremely simple programs without using traditional variables and assignment operator, but once you start thinking about slightly more complicated problems, things become difficult. Let’s look at the following function, which sums numbers in a specified range (this can be of course calculated directly, but I’ll use it as an example of a calculation which uses a loop):

int SumNumbers(int from, int to) {
    int res = 0;
    for (int i = from; i <= to; i++)
        res = res + i;
    return res;
}

In this case, we just can’t directly replace variable with value bindings, because we need to modify the value during every evaluation of the loop. The program needs to keep certain state and the state is changed during every execution of the loop, so we can’t declare a new variable for every change of the state. Thus we need to do a more fundamental change in the code and use a technique called recursion instead of using loops:

int SumNumbers(int from, int to) {
    if (from > to) 
        return 0;
    int sumRest = SumNumbers(from + 1, to);
    return from + sumRest;
}

As you probably already know, recursion means that a function (SumNumbers in our case) calls itself (in our case this is when we calculate a value for sumRest variable). In this code, we’re using only value binding, so it is using only purely functional features. The state of the computation, which was originally stored in a mutable variable, is now expressed using recursion. As you may guess from this introduction, the use of values instead of variables and keeping program state using recursion is an important feature whenever you want to write any interesting F# program.

1.3  Functions as values

Writing almost every program using recursion explicitly would be rather difficult, so functional languages have developed a ways that allow us to write the “difficult recursive part” of the program only once and use it in many variations for different purposes. How can we separate the functionality that will vary during every use from a recursive part of the code? The answer is simple – we will write the recursive part as a function with parameters and these parameters will specify what “unique operation” that the function should perform.

Let me demonstrate the idea on a previous example. We wrote a function that takes an initial value, loops through a specified numeric range and calculates a new “state” of the calculation during every iteration using the previous state and the current number from the range. In the function above we used zero as an initial value and we used addition as an operation that is used to fold the numbers in the range, so a resulting computation for a range from 5 to 10 would look like (((((0 + 5) + 6) + 7) + 8) + 9) + 10.

What if we now decided to modify this function to be more general and allow us to perform computations using different operations, for example multiply all numbers in the range and generate the following computation: (((((1 * 5) * 6) * 7) * 8) * 9) * 10? If you think about the differences between these two computations, you’ll see that there are only two changes. First, we changed the initial value from 0 to 1 (because we don’t want to multiply any result of a call by zero!) and we changed the operator used during the computation. To make the code more general, we’d like to write a method AggregateNumbers that takes the initial value as an argument and a function, which would specify the operation that is used for aggregating the numbers. This function should take two integers as an argument and should return an integer as a result.

We’ll see how to write a function like this in both C# and F# in the next section. The use of functions as an argument is called using functions as values, because we use a function in a place where other values are used such as method argument or return value. Hiding recursion in a function or method that accepts a function value as an argument is a very powerful technique and we’ll see it in the example demonstrating working with lists as well.

1.4  Immutable data structures

We already discussed that functional languages prefer to use value bindings instead of variables and we’ve seen how it influences the programming style. The approach not to use mutable values isn’t limited just to variables and extends to a declaration of all functional data types. Functional data types are usually immutable as well, which means that a value of the type cannot change. The only way we can change a value is by creating a copy with a modified value. Even though it may seem a bit strange for the first time, it isn’t actually that uncommon. An example that you already know is a string type, which is immutable in .NET. This means that all operations performed on strings return a copy and don’t modify the original value:

string input = "hElLo wOrLD!";
string first = input.Substring(0, 1).ToUpper();
string rest = input.Substring(1).ToLower();
string result = first + rest;

As you can see in this example, working with immutable data types is quite simple. Instead of modifying the value, we just declare a variable and store the new value returned by the operation in this variable and leave the original value unchanged. Of course, this approach can be used for other data types as well. Let’s look for example at the type for storing a collection of integers implemented as an immutable data structure:

FunctionalList list0 = FunctionalList.Empty();
FunctionalList list1 = list0.Add(1);
FunctionalList list2 = list1.Add(3);
FunctionalList list3 = list2.Add(5);
FunctionalList list4 = list3.Add(7);

To construct a list of integers, we need just two basic operations – on the first line, we need to create an empty list (called Empty) and in the rest of the example, we’re just adding element to the existing list, which is an operation (called Add in this example) that returns a new list composed from the original list and the new element. This previous example can be of course written more elegantly, without declaring all the unnecessary temporary variables. We could just call the Add operation straight away on the returned temporary list:

FunctionalList res = FunctionalList.Empty().Add(1).Add(3).Add(5).Add(7);

You’re probably thinking that copying the whole list every time we want to add a new member to the list is inefficient. This would be of course true, but we don’t actually have to copy the whole list. Let’s say that we have a list l1 containing 1, 2, 3 and want to append 0 at the beginning. Instead of copying the whole content of l1, we can simply create an object (for example l2) that contains the new value (0) and a reference to the original list (l2). This wouldn’t work for a mutable list, because if we modified some element in l2, it would also change the original list (l1). Since we’re working with immutable data structures, none of the lists can be changed, so keeping just a reference to the original list is a correct approach.

1.5  The absence of side effects

The use of immutable data types means that a code cannot perform any side-effect. By side-effect I mean for example modifying a value of global variable. A function written in this way is much closer to the mathematical notion of a function and is usually called pure function by functional programmers.

Functions like this are very interesting, because they have similar properties as mathematical functions. The only thing that the function can do is to return a value, which means that the order of evaluation is not important and evaluating a function two times leads always to the same result. This means that the following two examples perform exactly the same thing:

FunctionalList l = GetData();
return ProcessList(l) + ProcessList(l);

In the second version, we optimize the code to run the ProcessList function only once:

FunctionalList l = GetData();
int tmp = ProcessList(l);
return tmp + tmp;

Indeed, you would expect that this code does the same thing, but it isn’t always true in imperative programming, because ProcessList can modify some global variable, so running it just once instead of twice changes the meaning of the program.

So far I mentioned modifying global variable as the only side-effect, but to be a truly pure function (meaning that the result depends solely on the arguments), it also cannot perform any I/O operation, like reading from or writing to a file, communicating over the network or interacting with the user. In F#, you can do all these operations, but the way you write the code helps you to prevent from mistakes that can be caused by using side-effects in a place where you wouldn’t expect them.

Minimizing the use of side-effects is very useful if you want to have clearer way for thinking about the code, but it is also extremely valuable when developing applications that run on multi-core systems. We’ll see an example demonstrating why avoiding side effects is important shortly in section 4.

2  F#: The functional .NET language

Before we can continue our discussion about functional programming in general, let’s look at several practical examples in the F# language. As already mentioned, F# is a .NET language, so we can access . NET libraries, but there is also a lot of functionality in the F# libraries, that is suited especially for functional programming in F#.

To present F#, I decided to write several “Hello world” examples. We’ll start with the most classic version, which prints the message to a screen. To show something more complicated, I implemented two more “Hello world” examples that we’ll examine later. Next one presents a recursive function for calculating factorial, which is a “Hello world” example used in functional programming and the last one is a graphical “Hello world” showing how to use basic Windows Forms controls and event in F#.

F# can be downloaded from the F# Web site [2] and it contains integration with Visual Studio (you can even use the free Shell version [3]). In the following examples we’ll use the simplest way to play with F#, which is to use the F# interactive tool. It can be used either from console (fsi.exe) or from Visual Studio. After creating new F# project in Visual Studio, you can simply highlight a block of F# code and hit [Alt]+[Enter]. This command sends the selected text to the F# interactive window compiles it and executes it, so we can immediately see the results.

2.1  Imperative hello world

Let’s start with the first example from our “Hello world” series. The following listing shows the content of the F# interactive window after entering and executing a line of code that calls the printfn function, which is a function defined in the standard F# library:

MSR F# Interactive, (c) Microsoft Corporation, All Rights Reserved
F# Version 1.9.4.17, compiling for .NET Framework Version v2.0.50727

> #light
  printfn "Hello world!"
  ;;
Hello world!
val it : unit = ()

The first line contains a directive #light, which turns on the lightweight F# syntax – this is a syntax option that simplifies writing code a lot and we’ll use it in the rest of the article. Next, you can see a line of code with the printfn function followed by a two semicolons - two semicolons are used to terminate the input, so that you can enter multiple lines of text when writing the code directly in F# interactive. As you can see, after entering the command, the message “Hello world” appeared in the console window. Finally, the last line shows the result of the calculation. In F#, you can treat every block of code as a calculation with some result. In this case, the printfn function doesn’t return any value, so it just returns unit, which is something very similar to the void “type” known from C#.

2.2  Functional hello world

Let’s now look at more interesting “Hello world” example, which shows a calculation of the factorial function in F#. If you’re not familiar with factorial, it is a function that takes a number n and returns 1 when n is less than 2 and returns factorial of n – 1 multiplied by n otherwise:

> #light
  // Declaration of the factorial function
  let rec factorial num =
      match num with
      | n when n <= 1 -> 1            // First case branch
      | n -> n * (factorial (n - 1))  // Second case branch
  ;;
val factorial : int -> int

> // Testing the factorial
  factorial 5
val it : int = 120

The first command entered to the F# interactive is a declaration of the function to compute the factorial. The function is declared using let rec keyword. This specifies that we’re declaring something (let can be used for declaring simple variables as we’ll see later) and that we’re declaring something recursive (rec can be viewed as a modifier). These keywords are followed by the function name and by the arguments of the function (here we have just one argument called num) and by the equals sign.

The equals sign separates the function header from the body. In our example, the body is just one match expression. This is a very common expression in functional languages and represents the fact that we want to take the value (num in our case) and test whether it satisfies some condition (in a functional terminology we’d say whether it matches a certain pattern) and select the according code branch. In our example, we have just two patterns. The first pattern assigns the value to a variable called n and tests whether n is less than or equal to one. This is written as an additional condition using when clause. The second patter simply assigns the value to a variable called n and doesn’t perform any additional test, so it matches all the remaining situations. The code for both branches is separated by the arrow sign (->) and either directly returns a value, or performs the recursive call and multiplication.

This code demonstrates one more essential F# feature, which is type inference. If you look at the result printed on the next line, you can see that we declared a function that takes int as an argument and returns int as a result. This may be surprising, because we didn’t specify the type anywhere! What the F# compiler did is that it analyzed the code. It can see that in the first branch, we’re returning a value of type int (constant 1), so it deduced that the return type is an integer. Similarly, we’re subtracting one from the argument n in the second branch, which means that the argument num itself should also be an integer. The type inference mechanism in F# is quite advanced and as you can see it attempts to deduce as much as it can automatically. We’ll talk about type inference in some more detail later in the article.

2.3  .NET hello world

To finish our quick tour of F#, let’s look at simple example that creates Windows Forms “Hello world” application. It creates a simple form with a label on it. You can see the source code in the following listing with a screenshot of the running application below:

> // Import useful .NET namespaces
  open System
  open System.Drawing
  open System.Windows.Forms

  // Create the form and a label objects
  let frm = new Form(Text = "Hello world!", Height = 150)
  let lbl = new Label(Text = "Click here!", Dock = DockStyle.Fill, 
                      TextAlign = ContentAlignment.MiddleCenter)

  // Set ‘Font’ property of the label and add label to the form
  lbl.Font <- new Font("Calibri", 24.0f)
  frm.Controls.Add(lbl)
  frm.Show()
  ;;

val frm : Form
val btn : Label

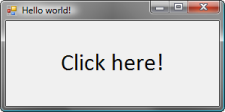
This example demonstrates several F# features that are essential for accessing .NET components. First, you can see the use of open keyword, which makes types from a .NET namespace available in the code, so we don’t have to use full names.

The next block demonstrates creating the controls. This is done by creating standard .NET objects using the usual new keyword for creating objects. As you can see, we’re using the let keyword again, but this time it is used to declare a local value (similar to variables from imperative languages), so here we declare values frm and lbl that hold the reference to our objects representing the controls.

When creating an object instance in F#, it is also possible to specify some properties of the object directly during initialization. You can see this for example in the code that creates the form – the comma separated assignments that are specified after listing all arguments to the constructor (in our case there aren’t any arguments) specify additional properties of the object. For example Text = "Hello world!" when creating the form specifies that the Text property should be initialized with the given string. After that, we set the Font property of the label, which is done using operator written as <-, so keep in mind that ordinary equals sign (=) in F# is a comparison that returns bool value and not an assignment! Finally, we call two .NET methods to add label to the form and show the form. If you want to turn this code from an F# interactive script into a Windows application, you’ll have to use Application.Run instead of frm.Show.

Using F# interactive has one interesting advantage – we can develop the program in an iterative style, meaning that we can write some code, immediately see the result and then add some features and see how it affects the running program. This is exactly what we’re going to do next – we use the previous example and add some event handling to the code:

> // Create random number generator
  let rnd = new Random()   

  // Function that changes the text of the label and back color of the form
  let handleClick (e:EventArgs) =
      let r = rnd.Next(256) 
      let g = rnd.Next(256)
      let b = rnd.Next(256)
      // Set the text and the new back color
      lbl.Text <- if (lbl.Text = "Tock!") then "Tick!" else "Tock!"
      frm.BackColor <- Color.FromArgb(r, g, b)

  // Add ‘handleClick’ as an event handler to the label
  lbl.Click.Add(handleClick)
  ;;
val rnd : Random
val handleClick : EventArgs -> unit

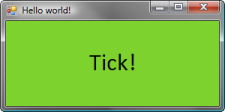
The code first creates a standard .NET random number generator object, which is then used in the handleClick function for generating a new color of the background. This function will be later used as an event handler for the click event of the label. It takes single argument, because we need to make it compatible with the code for attaching functions as event handlers below. As you can see the argument e isn’t used anywhere in the code, so I added type annotation (e:EventArgs) to specify what is the type of the argument. Actually, the code would work without the type annotation as well thanks to the automatic use of generics in F#, which I’ll talk about shortly later, but I wanted to make it as simple as possible for now.

The next interesting thing is that we’re using if … then … else as an expression, which is not usual in imperative languages. Here, the return value of the if … then … else expression is a string and it can be either "Tick!" or "Tock!" depending on the currently displayed text. Finally, we use the Add method of the Click property to add the function as an event handler for the event. F# works with . NET events in a slightly different way than C#, so there is no need to create a delegate explicitly. We can just use directly the function name or even lambda function, which I’ll talk about shortly.

3  Real-world functional programming

In this section, we’ll look at some practical uses of the functional programming concepts introduced in the first section. I’ll start with an example that I already talked about in the first section – that is using functions as arguments to other function in both C# 3.0 and F#. Next, I’ll show you why generics are so important for F#. Finally, we’ll look at some interesting examples that demonstrate how close LINQ in C# 3.0 is to the F# functions for working with collections of data.

3.1  Functions in F# and C# 3.0

Let me just shortly remind you the example that I used earlier when talking about functions in the first section. We started with a code that sums all numbers in a specified range. You can see our original code in the following listing:

int SumNumbers(int from, int to) {
    if (from > to) 
        return 0;
    int rest = SumNumbers(from + 1, to);
     return from + rest;
}

The question that we faced was: “How can we make the code more general?” In particular, we wanted to extend the function so that it could either sum all numbers in the range or multiply all numbers in the range.

Calculating using functions in C#

To do this, we need to add two additional arguments to the method. The first argument should specify the initial value (as we need to use 1 as a default value instead of 0 when multiplying numbers) and the second argument should specify the operation that should be used on the last line when we’re calculating a result from variables from and rest. Let’s start by looking at the solution in C# language (using the 3.0 version):

int AggregateNumbers(Func<int, int, int> f, int init, int from, int to) {
    if (from > to) 
        return init;
    int rest = AggregateNumbers(f, init, from + 1, to);
    return f(from, rest);
}

Func is a delegate that is defined in System namespace in .NET 3.5. As you probably already know, delegates in .NET are something like a type-safe pointer to a method. This means that we can use delegate for giving some piece of executable code as an argument to other methods. Func in particular is a generic delegate, so we have to provide it with type arguments. Type arguments specify what the parameters and return value of the referenced piece of code are. Just for a review, here is a declaration of the delegate (showing also similar delegate written without generics):

// Declartion of the generic Func delegate with 2 arguments 
delegate TResult Func<T1, T2, TResult>(T1 arg1, T2 arg2); 

// Instance used in our example earlier (without generics):
delegate int Func_IntIntInt(int arg1, int arg2); 

Delegates can be used similarly as methods in the code, so on the last line of the AggregateNumbers, we simply invoke the delegate value f instead of adding the numbers using plus operator. In functional programming, we don’t talk about “delegates”, but we work with a simpler concept – a function. In a pure mathematical understanding, function is simply something that takes arguments and returns the result. Indeed, this is exactly what the delegate represents in this example. As we’ll see shortly, in F# we don’t have to use delegates to implement this example and we can use the basic ‘function’ concept directly.

Before looking at the F# version, let’s look at the code that calls AggregateNumbers to perform the two tasks discussed earlier (adding and multiplying numbers in a range). Of course, we could write methods with a compatible signature (for example AddInts and MulInts) and use them as the arguments. Unfortunately that wouldn’t make the code shorter. What we want to do instead is to specify the argument to the AggregateNumbers directly when calling the method. To do this we can use new C# 3.0 feature called lambda functions (which is an extension and simplification of anonymous delegates that appeared in C# 2.0):

// Aggregate numbers using "+" and using "*" operators
int r1 = AggregateNumbers( (a, b) => a + b, 0, 1, 5);
int r2 = AggregateNumbers( (a, b) => a * b, 1, 1, 5);

// Outputs: "add: 15, mul: 120"
Console.WriteLine("add: {0}, mul: {1}", r1, r2);

You can see two examples of lambda functions on the first two lines. The arrow symbol (=>) separates specification of arguments (on the left side) from the body expression on the right side. In both examples, we define a function that takes two arguments (called a and b) and performs some simple calculation with them on the right side.

Lambda functions are another important feature of functional languages. They give us a very simple way to write a function “inline”, so that we can use it as a parameter to method that takes delegate as an argument (in F# it will be just a function instead of delegate). This is particularly useful if the function is simple and isn’t used anywhere else in the code, which is exactly the case of our previous example. Functional programming also uses functions (or delegates) as parameters of other methods quite often, so using lambda functions is very common.

Calculating using functions in F#

Let’s now look at exactly the same code implemented in F#. Of course, in F#, we’ll implement aggregateNumbers simply as a function using let rec keyword instead of method in some class:

> let rec aggregateNumbers (f:int -> int -> int) init nfrom nto =
      if nfrom > nto then init else
          let rest = aggregateNumbers f init (nfrom + 1) nto
          f nfrom rest
  ;;
val aggregateNumbers : (int -> int -> int) -> int -> int -> int -> int

Most of the code is similar to the previous C# version. It contains if expression with then branch that returns the initial value (init) and an else branch. The else branch first recursively processes the numbers in a range skipping the first number and then calculates the aggregate value from the first number (nfrom) and recursively calculated result (rest).

What is however interesting is the parameter f, which is a function used for aggregating the numbers. In the header of the function, I added type annotation to it, so that we can see what the function type looks like: int -> int -> int. This syntax represents a function that takes int as a first argument, another int as a second argument and returns int as well. This is similar to the delegate type that we’ve used earlier. You can also see the type of the whole function aggregateNumbers (printed by the F# interactive). It starts with the type of the f parameter (in braces), followed by three integers. The return type is of course also an integer. To call it, we’ll again use lambda functions, but this time in F#. This represents exactly the same idea as the previous C# version, but with a slightly different syntax:

> aggregateNumbers (fun a b -> a + b) 0 1 5;;
val it : int = 15

In F#, lambda functions are written using the fun keyword, which is followed by the declaration of arguments (in our example a and b). The header is ended with a single arrow symbol (->) and then follows the body of the function.

Making functions using partial application

Now we’ve implemented a more general version of the function, which is certainly very useful. On the other side, if we wanted to use it for adding numbers (as sumNumbers did) very often, we’d prefer to declare the more specific function (sumNumbers) as well, so we wouldn’t have to write the additional arguments in every call.

In F# this can be done using partial application, which is also sometimes called currying. It means that we specify only first few arguments of the function and the result will be a function that takes only the remaining arguments. In our case, we’ll specify only the operator for aggregation and the initial value:

> // Declare 'sumNumbers' and 'mulNumbers' using partial application
  let sumNumbers = aggregateNumbers ( + ) 0
  let mulNumbers = aggregateNumbers ( * ) 1
  ;;
val sumNumbers : (int -> int -> int)
val mulNumbers : (int -> int -> int)

> // Test the returned functions:
  sumNumbers 1 5;;
val it : int = 15
> mulNumbers 1 5;;
val it : int = 120

On the first two lines, we use partial application to create two specialized functions using aggregateNumbers. Also note that in F# we can use ordinary operators as parameters. This means that instead of writing the code using lambda function, which calls the operator, we can simply use the operators themselves.

If you look at the signatures printed by the F# interactive, you can see that both sumNumbers and mulNumbers have type int -> int -> int. This is exactly what you get if you “cut off” first two arguments from the aggregateNumbers function. And, as you probably already know, this represents a function that takes two integers (representing the range) and returning an integer.

I think that now you know enough about functions and we can look at some examples where we can use them for some more real-world example. In the next section, I’ll briefly talk about the relation between F# functions for working with collections of data and similar functionality now available in C# 3.0 and LINQ.

3.2  Functional lists and LINQ

Since this article is just a short introduction to functional programming, I will not discuss everything in detail (you can find much more information in the book). In particular, I won’t explain how lists are implemented in F# and how you can manipulate with them on the lowest level – that is accessing elements of the list, constructing lists programmatically and so on.

Instead, I’ll demonstrate several interesting similarities between lists in F# and working with collections of data using new C# 3.0 features and LINQ project. This part will demonstrate two things – first, you’ll see how using the new C# 3.0 features makes many daily task easier and second, you’ll see that these new features are directly motivated by functional languages. Later, we’ll see that in functional programming, the same approach is often used also for solving problems other then working with data. The point of the functional style is to make the code more declarative. This means avoiding as many technical details that are not relevant for the problem as possible.

Creating lists

Before we can start manipulating with lists, we’ll need to initialize some. In F#, we’ll also reference module called List, which contains useful functions for working with lists (module is something like a namespace, but it can contains functions and not only classes). Similarly, in C# you’ll need to add using directive for the System.Linq namespace, which contains LINQ functionality for working with collections.

The code that references List module and initializes list called l in F# looks like this:

> open List;;
> let l = [ 1 .. 10 ];;
val l : int list = [1; 2; 3; 4; 5; 6; 7; 8; 9; 10]

The list is written in square brackets and can be written by listing all the elements as you can see on the last line, where F# interactive automatically printed the value. We’ve used a second option, which is a simplified notation for creating list containing a range of numbers. In C#, we can use collection initializers to write very similar code:

var l = new List<int> { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };

Collection initializers are new feature of C# 3.0 and allow us to use similar expression when initializing (built-in) arrays and when initializing custom collections. This is very simple feature, but has been available in many functional languages for a long time.

Filtering and projection

In the upcoming two sections, we’ll look at basic examples of manipulating with items in the list. As I already mentioned, the functional data structures are immutable, which means that all the operations do not actually modify the existing data structure. Instead they return a new list. The examples that demonstrate LINQ in C# use IEnumerable<T> type, so the returned value is calculated on demand (only when we enumerate it using something like foreach), but the idea is essentially the same.

In both cases, we get a new value representing the new data and the original list is not altered in any way. In F#, this isn’t possible, because the list is truly immutable and in C# we don’t do it, because we want to use data collections in a functional way. In section 4 I’ll shortly discuss the key reasons why using immutable structures is a good idea, but now, let’s look at the code.

The first example demonstrates two operations – filtering and projection. Filtering means that we select only elements that fulfill some condition (for example, whether a number is a multiple of three) and is similar to the WHERE clause from SQL. On the other side, projection is similar to the SELECT clause. We can use it to perform some calculation for every element in the list and get a list containing results of these calculations (for example, we can multiply all numbers in the list by two). The code for this is surprisingly similar, so you can see both F# and C# version side by side:

> // Select multiples of three
  let l1 = filter (fun n -> n%3 = 0) l;;
val l1 : int list = [3; 6; 9]

> // Multiply every element by two
  let l2 = map (fun n -> n*2) l1;;
val l2 : int list = [6; 12; 18]    

// Select mutiples of three
var l1 = l.Where(n => n%3 == 0);
// result l1: [3; 6; 9]

// Multiply every element by two
var l2 = l1.Select(n => n*2);
// result l2: [6; 12; 18]

To perform filtering, we use a function called filter in F# and an extension method Where in C# 3.0. Both of them take a lambda function that specifies the condition as an argument. Note that the lambda expression takes a single argument (the element in the list) and returns a boolean value specifying whether the condition was satisfied or not. When using the extension method in C#, the list is specified by the value preceeding the “dot” symbol and in F#, it is specified as a last argument of the function. The second example, which demonstrates projection is very similar. The only diference is that the lambda function takes a number as an argument and returns also a number. The results are collected into a list, so we get a list of numbers (l2) as a result.

Processing lists in a pipeline

In the previous examples, we wrote filtering and projection as two separate calls that took some input and returned a collection as a result. This works fine, but it would be more elegant if we could write this as a single operation without declaring an additional variable to store the temporary result.

We can do this simply by “cutting” the first expression and “pasting” it in place of the temporary variable (l1). As you can see in the following listing, the C# version already looks very readable, but we’ll still have to do some improvements to the F# version:

> map (fun n -> n*2) 
      (filter (fun n -> n%3 = 0) l)
  ;;

val it : int list = [6; 12; 18]

var it = 
  l.Where(l, n => n%3 == 0)
   .Select(n => n*2);

// result it: [6; 12; 18]

The C# version looks elegant, because we were already using extension methods that were added to C# 3.0 exactly for this purpose. If you try to imagine how you’d write the same thing using ordinary static methods like Utils.Where, you’ll see that it would be similarly confusing as our current F# version.

One of the advantages of using extension methods in C# is that we can write the method calls in the order in which they are executed (first Where – filtering and then Select – projection). In the previous F# version the operations were written in a reverse order. Of course, F# offers a solution for this problem. The solution is to use pipelining operator (written as |>), which allows us to write a sequence of operations:

> l |> filter (fun n -> n%3 = 0) 
    |> map (fun n -> n*2)
  ;;
val it : int list = [6; 12; 18]

Using the query operator, we get a similar structure of the code as we had in the previous C# 3.0 version using extension methods. The pipelining operator is a binary operator and its meaning is that the value on the left side is used as an argument to the function on the right side. Thanks to the associativity rules, the operations are performed in a sequence, meaning that the first operator (preceding filter) is executed before the second one (preceding map).

In F#, it is possible to define custom operators and pipelining operator is something that you could very simply implement on your own. It is however extremely useful, so it is part of the standard F# library. As you probably know, custom operators cannot be declared in C#, but extension methods provide often an interesting alternative. As this example demonstrated, we can get very similar result by using extension methods (Where, Select) in C# and pipelining operator (|>) in F#.

Embedded query language

To close our short excursion to the world of data collections, we should also look at query expressions that are available in C# 3.0 and let us write a query like the previous in a form that is syntactically similar to SQL. You should however keep in mind that this is just a syntactic sugar and the code is translated to exactly the same code as we’ve used in the last example:

var it = 
    from n in l
    where n % 3 == 0
    select n * 2;

F# has a more general feature that can be used for writing computations like this, which is called sequence expression. The interesting thing is, that in F# this is a more general language feature (the generalized version is called computation expressions). This means that you can use it not only for working with lists (let’s call these list computations), but also for other kinds of computations. One interesting example that is further described in our book is using computation expressions for writing code that executes asynchronously (e.g. when downloading data from internet using HTTP requests).

I’ll not demonstrate sequence expressions here, but there is still one thing that I’d like to show you. There is one interesting option for making the previous F# code even more compact and that is using partial application (or currying), which I shortly introduced earlier:

l |> filter (fun n -> n%3 = 0) 
  |> map ((*) 2)

You can see that we did a change to the second line and instead of using lambda function as a parameter we used an expression ((*) 2). What does this code represent? Well, asterisk is an operator for multiplication, so if we had a function mul that multiplies two numbers, the expression would mean the same thing as: (mul 2). Here, we’re getting back to partial application – the function mul takes two numbers and returns their product. In this code, we give it only a single argument, so it instead creates a function that takes a number as an argument and multiplies it by two. This means that we get exactly the same functionality as earlier. If you’re still a bit confused by partial application, you can imagine that the compiler automatically inserts a function that takes the second argument for the mul function. The code with this modification would be (fun n -> mul 2 n), which is exactly what we wrote earlier.

3.3  Generics in .NET 2.0 and type inference in C# 3.0 and F#

In the previous section we looked at working with lists and we’ve seen several examples of using F# functions and C# extension methods for working with collections. In particular, we examined filter (and C# equivalent Where) and map (Select in C#).

One thing that is extremely interesting about these methods is that they work with any type of list or collection. This means that we can use the same function for filtering a list of strings as well as a list of integers, floating point numbers or for example types representing products. The mechanism that makes this possible is called generics and is available in C# since version 2.0. In F# this mechanism is essential for writing any real-world piece of code.

In functional programming the type signatures of a function (especially if the function is generic) serve as a very useful hint when writing the code. In the next few paragraphs I’d like to show how you can “read” the type signature and use it for understanding what the function does and functions for working with collections are excellent example for this. Let’s first look at declarations of the C# extension methods that we were using:

// Filters elements of ‘source’ based on ‘predicate’
IEnumerable<T> Where<T>(IEnumerable<T> source, Func<T, bool> predicate);

// Projects each element in a sequence ‘source’ into a new form using ‘selector’
IEnumerable<R> Select<S, R>(this IEnumerable<S> source, Func<S, R> selector);

The first method has a single type parameter (called T), which represents the type of elements in the collection to be filtered. This means that the type parameter is used in the type of the first parameter (IEnumerable<T>). The second parameter represents a function which takes a value of type T as an argument and returns a bool and is used as a predicate when filtering the elements.

You may already know that when you call a generic method as we did in previous examples, the type parameter is replaced with the actual type (in our examples the actual type was int). This can be either done explicitly by writing Where<int>(...). In this case we just write the type that should be used instead of the type parameter. However, C# is sometimes able to infer the type of the type parameter, so we don’t actually need to write it. That’s how all our previous examples worked. We simply wrote Where(src, f) (where src and f were some expressions with a known type) and C# compiler used the type of src and f to deduce the type for the type parameter. This mechanism for deducing types based on the context is called type inference and I already shortly talked about it when we were looking at F# “Hello world” examples.

Let’s now look at the signatures of filter and map functions in F#. We can do this simply by entering the names of the functions in the F# interactive. This is because a function is also a value in F# (it is a value of type function) and when we enter any value in the F# interactive, it prints its type and the value. A function is just some compiled code, so it cannot be reasonably printed, but we’re interested in the type:

> List.filter;;
val it : (('a -> bool) -> 'a list -> 'a list) = <...>
> List.map;;
val it : (('a -> 'b) -> 'a list -> 'b list) = <...>

In this example, I entered the full name of the function including a module name. In our discussion of C# versions, I talked about Where (equivalent to filter), so this time, I’ll focus on the second one. In the C# version a method for projection had two type parameters. It was declared as Select<S, R>, where S was a type of the elements in the source collection and R was a type of the elements in the resulting collection.

To distinguish between ordinary types and type parameters, F# uses slightly different syntax, so if you look at the signature of map, you can see two type parameters: 'a representing the source type and 'b representing the result type. F# also allows different syntax for instantiation of generic types (that is specifying the type for generic types), so 'a list means exactly the same thing as list<'a>. The following diagram shows in detail what the signature means:

If you think about the type, you can easily come to conclusion what the function does. It takes a list containing some values of type 'a. The code is generic, which means that it doesn’t know anything about this type and without any other argument it wouldn’t be able to do anything with a value of this type. However, another argument specifies a function that can transform a value of type 'a into a value of type 'b. This suggests that the function could iterate over all elements (of type 'a) in the list and transform all of them into values of type 'b. Finally, we also know that it returns a list containing elements of type 'b, so we can easily guess that the function performs projection. This kind of reasoning is often very useful, because it makes reading functional code very easy. You can apply similar reasoning to filter as well and you’ll see that the only thing it can do is to test whether every element in a list should be contained in the result using the specified predicate.

Automatic generalization

The most important difference between generics in C# and similar mechanism in F# is that in F# you don’t have to explicitly say that the method is generic when you write it. You can do it, but in most of the cases you don’t have to, because the compiler makes it generic automatically. This is topic that would require much more space, but it is very important, so I’d like to quickly introduce it.

Let’s look at a very simple C# implementation of Map method. The following code works with List<T>, so it is different from the previous examples, where we were working with LINQ methods that take general IEnumerable<T> type. Nevertheless, it is a good example for demonstrating automatic generalization in F#:

List<R> Map<S, R>(Func<S, R> f, List<S> source) {
    List<R> res = new List<R>();
    foreach (S el in source) 
        res.Add(f(el));
    return res;
}

As you can see, we explicitly defined two generic type parameters (S and R) and used them in the method header (for defining types of arguments f and source) and also in the body (when declaring res and in the foreach loop). I will not show how the code looks in F#, because we haven’t seen any examples of functions working with lists (this is unfortunately out of the scope of this article), but I’ll demonstrate how we could write this in a non-existent functional pseudo-C# language. First, I’d like to shortly recapitulate one new feature in C# 3.0 – a new keyword var, which can be used for declaring local variables in a method body:

var n = 10;

The var keyword simply instructs the compiler to look at the expression assigned to the variable and infer the type of the expression. In our case, the expression is a constant of type int. The compiler then uses the type as a type of the variable (in our case n). This means that the variable will be ordinary, statically-typed variable (or type int in our example), but we don’t have to write the type explicitly. In C#, this feature is called type-inference. In the pseudo-C# language that I made up to demonstrate automatic generalization, you can use var almost anywhere, where a type is expected, so you can write the following code:

var Filter(var f, List<var> source) {
    var res = new List<var>();
    foreach (var el in source) 
        res.Add(f(el));
    return res;
}

The compiler for pseudo-C# has to be quite smart – at the beginning it only knows that source is a list containing elements of some unknown type. The compiler could assign it some name, for example T1. Then it also knows that the foreach loop iterates over all elements in the source, so the type of el should be also T1. Next, it sees that we’re using the argument f as if it were a function and that we’re adding the returned values to a list res (containing elements of some unknown type). From this, it infers that f is a function taking T1 and returning something (let’s assign it a name T2), so it has to be of a type Func<T1, T2>. Similarly, we now know that res is of type List<T2> and also that the return type of Filter is List<T2>. Because there are two newly named types (T1 and T2), the compiler now know that the method is generic and has two type parameters.

This kind of reasoning is just a much more advanced variant of type-inference and is used in many functional languages including F#. Thanks to the different syntax of F# language, the code doesn’t look as odd as the code in the pseudo-C# (with var keyword almost everywhere). In F#, you just don’t have to write the types if you don’t want to change the type automatically inferred by the compiler. The type inference mechanism not only makes the code more generic automatically, but also often helps to catch a mistake. If the inferred signature is different from what you’d expect, you can see that there is something wrong with the code.

4  Functional architecture

In this last section, I’d like to shortly talk about architectural aspects of functional programming. This would of course require an entire article (more likely even a longer book than our Real-world Functional Programming), but I’d like to conclude this article with a short look from a high level – to balance the low level look from the previous sections where I was talking mostly about language features.

4.1  Immutable data structures and parallelism

The first thing that you learn when using functional programming is that you start the development of any functional program by thinking about the structure of the data that the program uses. For example, when developing a game, you don’t think about the objects that are in the game and about the functionality that each object provides. You think about the data structure that could represent the world, structure that could represent the characters in the game and so on. Please, keep in mind that this is a very simplistic example and it doesn’t cover all the complexity of a real-world development. It is however advanced enough to show some important aspects of functional programming, which is exactly a reason why I’m discussing it in this section.

We didn’t talk about common functional data structures in this article, but you can find a good overview in my article [4]. Of course, an entire section of our book focuses on the problem of structuring functional programs. However, we did introduce one functional data structure in this article and that is list, so we can for example imagine that in a game, we have a list storing information about all characters in a game:

> // Stores information about computer controlled agents in the game
  type GameCharacter = ... 

> // List with all characters currently in the game
  let characters = [ ... ]
val characters : GameCharacter list

There is some type called GameCharacter that represents a single AI character controlled by the computer. This type would store all the necessary information about the character. Next, we have a list containing all the characters. This list would be probably a part of some type representing the whole virtual world, but in our simple example, we’ll just work with this list. The next thing to do is to define functions for working with GameCharacter type. Simplest functions that we may need are a function to update the character – that is to perform a single step in the game, like moving the character, and a function that tests whether the character is still alive (or whether it died for some reason during the last update):

> // Calculates a new position, etc. of the character
  let updateCharacter ch = ...
val updateCharacter : GameCharacter -> GameCharacter 
> // Tests whether the character is alive
  let isCharacterAlive ch = ...
val isCharacterAlive : GameCharacter -> bool

Now that we have the data structures that represent our game and several basic functions that define operations on them, we can write an elementary step in our game. We’ll write a function updateCharacters that takes a list of game characters, performs update on each of them and removes all characters that died during the update. Since we’re using a list as a data structure to store our characters, we can of course use previously discussed functions for working with lists:

> // Updates all characters and removes those who died during the last update
  let updateCharacters characters = 
    characters
        |> map updateCharacter
        |> filter isCharacterAlive
val updateCharacters : GameCharacter list -> GameCharacter list

The data structure to store characters is immutable, so the updateCharacters function takes a list with characters (representing the current state) and returns a new list without modifying the original one. This approach has several important benefits. First of all, it is much easier to understand what the code really does – if you see a function that takes a list of characters and returns a list of characters, you can safely assume that it doesn’t modify any other part of the world than the characters. In the previous example it is also guaranteed that the updateCharacter doesn’t do anything else then just calculating a new state of the character from the previous one. It might read some properties of the state stored globally, but it cannot alter it. As we’ll see in the next few paragraphs this is an extremely useful property for dealing with recent trends in the computing industry, such as multi-core processors and multi-processor systems.

Parallelization of functional programs

Let’s now imagine that we want to make the previous code multi-threaded. Updating the state of the character may be an expensive operation (especially if it involves some AI), so we’d like to use multiple threads to calculating new state of the characters. It turns out that doing change like this is astonishingly simple:

let updateCharacters characters = 
    characters 
        |> parallelMap updateCharacter
        |> parallelFilter isCharacterAlive

In this example, we just changed call to map with a parallelMap and similarly replaced filter with parallelFilter. These new parallel functions do exactly the same thing as their non- parallel versions, but their implementation is more advanced and performs the operation on multiple threads instead of doing it sequentially.

How is it possible that adding multi-threading is that simple in this example, while doing similar thing in imperative object-oriented code is difficult? The first key difference is that the functional program we’ve written is very declarative – it separates the functionality that knows how to process a list into high-order functions (map and filter) and the user code just defines what should be done with the list (updateCharacter and isCharacterAlive in our example). The second key feature is that we use immutable data structures, so changing the code from sequential to parallel cannot introduce any race conditions. I’ll talk about this in a more detail shortly.

Currently, functions like parallelMap and parallelFilter are not part of the standard .NET or F# library, but with the upcoming Microsoft Parallel Extensions to .NET [5] these will be available for LINQ and there will be bindings for F# as well. In the meantime you can either download a preview version or implement these functions on your own (for more information you can refer to my earlier article [6]).

Using the preview of Parallel Extensions to .NET we can write the same thing in C#. Assuming that we have a list of characters and methods UpdateCharacter and IsCharacterAlive, we can rewrite the previous F# code to C# as follows:

List<GameCharacter> UpdateCharacters(List<GameCharacter> characters) {
    return characters
            .AsParallel()
            .Select(UpdateCharacter)
            .Where(IsCharacterAlive);
}

Without the call to AsParallel method, it would look like an ordinary code for working with collections from our earlier examples. The AsParallel method, which comes from the Parallel Extensions library, hides a surprising complexity and as we can see, it exposes it in a very simple way. It changes a type of the collection that we’re working and provides a new implementation of Select and Where for this type. This means, that similarly as in the F# example, the code is using a different version of these methods that define how to work with collections. The implementation used in this example thanks to AsParallel uses multi-threading, so the processing is executed in parallel.

Of course, changing the code from a sequential version to parallel requires that UpdateCharacter and IsCharacterAlive don’t modify any global state in an inconsistent way. If the code relied on the fact that it is executed sequentially, adding AsParallel would break it. In functional languages, this is not a big problem, because the data structures are usually immutable, but in C# you need to be more careful. Even though, C# doesn’t directly support writing immutable data structures, you can implement many types in a functional way, which makes it possible to safely use this technique for making code multi-threaded. For more information about implementing functional data structures in C#, you can refer to a series of articles by Eric Lippert [7].

This example nicely demonstrates how architectural ideas from functional programming influenced technologies that are being currently developed to deal with issues like multi-threaded development such as Parallel Extensions to .NET. There are of course other technologies influenced by functional programming, but concurrent and asynchronous programming is very important nowadays, so these examples show why functional programming matters for a real-world developers.

4.2  Programs as languages

So far, we’ve discussed how functional programs are structured. I wrote that developing of functional program starts by designing the data structures and by designing operations that work on top of these structures. In this section, I’ll shortly talk about different way of thinking about functional programs and especially functional libraries.

Based on the earlier examples of F# you could see that the language has a minimum of predefined constructs. For example, we’ve seen that the same keyword let is used for declaring local values as well as for declaring functions. The rationale behind this is that a local value can be treated as a function that doesn’t take any arguments – not surprisingly, this is the way constants are usually defined in mathematics.

Thanks to the syntax of F# (and the same is true for many other functional languages as well) it is possible to define many typical constructs not as a built-in language feature, but as a custom operator or a library function. This means that you can implement a set of primitives and use them to construct your programs. The programs will then look as if the primitives were standard part of the language. We’ve already seen an example of this when working with lists – the pipelining operator (|>) is something that looks like a language feature, but it is just an ordinary F# operator.

Functional animations

Let’s now look at a more advanced example that shows what this means in practice. The following example demonstrates a “language” for describing animations in a functional way from Chapter 20 of our book:

let solarSystem = 
  sun
    -- (rotate 80.00f 4.1f mercury)      
    -- (rotate 150.0f 1.6f venus)        
    -- (rotate 215.0f 1.0f 
           (earth -- (rotate 20.0f 12.0f moon)))    

Even without knowing anything about F#, you could probably see what the program describes. It defines our solar system with the first three planets (Mercury, Venus and Earth with Moon) and defines how the cosmic objects rotate round each other. If you think about the code for a while, you can see that Moon rotates around the Earth and Earth, together with two other planets, rotates around the Sun. The rotation is specified using two numbers and if you could play with the program, you would quickly recognize that the first number specifies how far the planet is from the center of rotation and the second specifies how fast it should rotate.

In my opinion, the most surprising fact about this example is that if you didn’t know that the code is written in F#, you could think that it is written in some kind of simulation language. You could think that rotate is a keyword of this language (that defines how things rotate around each other) and that -- is some connector used in simulations. In fact, rotate is ordinary F# function and -- is a custom operator.

Language for working with lists

We can apply the same thinking to our earlier examples of working with lists. In the example with planets, the language defined two primitives – a rotate function and an operator -- for describing connections. The code that we implemented using these primitives is a model of an animation. In our case solarSystem is a model of an animation of our solar system. The language also knows how to execute the models. In the example with animations, executing a model means drawing the animation on a form.

In the examples for working with lists, we’re modeling transformations of lists. The primitives that are available to us are pipelining operator (|>) and basic functions for list manipulations (filter, map and many others). The transformation is described by parameterizing these basic functions (e.g. by specifying what items from the list should be filtered) and composition of the parameterized functions. We can for example model a transformation that takes a collection of customers, filters those who live in London and returns a collection of their names:

let res = 
  customers 
    |> filter (fun cust -> cust.City = "London") 
    |> map (fun cust -> cust.Name)

The code is very similar to our earlier examples for working with lists. This is because we’re using the same language for solving the problem. One more important note about this approach is that once a developer learns the language, he or she can very easily read and write code that solves problems for the problem domain for which the language was designed.

The last topic that I’d like to shortly discuss is how the models can be executed. In some situations it is desirable to provide more ways for executing the problems implemented using a same “language”. Actually, we’ve already discussed this when talking about parallelization, because one possible alternative is to execute the transformation in parallel. Another alternative way is to execute it as an SQL query using a database engine. The following example shows how we could implement these two alternatives in F#:

// Executing a ‘query’ on in-memory data in parallel
let res = 
  customers 
    |> parallelFilter (fun cust -> cust.City = "London") 
    |> parallelMap (fun cust -> cust.Name)

// Executing a ‘query’ on database by translating it to SQL
let res = 
  SQL <@@ %db.Customers 
           |> filter (fun cust -> cust.City = "London") 
           |> map (fun cust -> cust.Name) @@>

The first example uses parallelFilter and parallelMap primitives that we already discussed. The second uses F# quotations, which provide a way for supplying a completely different execution method for a piece of F# code. In this case, the SQL function takes the F# code enclosed between <@@ and @@>, translates it to SQL code and executes it as a database query. This example shows just the basic concept and you can find more information about quotations and F# integration with LINQ that allows this online (more on quotations can be found in [4], examples of real-world database queries in F# in [8]).

Domain specific languages

The approach to define some basic constructs is very popular and powerful. In context of F# it is called language oriented programming and these languages are called DSLs (domain specific languages) by some architects. This indicates that we’re defining a language for some problem domain and this language gives us a vocabulary and in some sense also grammatical rules for constructing our models. Of course, there are techniques for implementing DSLs in other programming paradigms, so the term can be for example used in OOP as well. However, as you could see, the flexibility of functional languages makes it possible to define a very succinct and expressive “language”.

Thanks to the vocabulary and grammar rules it can be often used even by those who understand the problem domain, but are not experts in functional programming. This means that those who use the DSL can be a distinct people from those who design it and develop it. Indeed, there are different requirements for people in both groups – the designers should be more advanced functional developers, whereas for the users, it is more important to well understand the problem domain.

5  Summary

In this greenpaper I wanted to show you some of the wonders of functional programming. Indeed, we didn’t have a space to look at more than a few selected topics and we couldn’t look at everything in detail, but I hope that the article convinced you that functional programming is an interesting and elegant paradigm, but also that it is very useful and can solve real-world problems as well as deal with current trends in the IT industry. Problems that can be nicely solved using functional programming include development for multi-core systems and the need to write the code in a more declarative and expressive way.

In this article we started with discussing the general concepts that are important for functional programming. We’ve seen that functional programs usually work with immutable declarations, how to use recursion as a primary control structure. We also looked at functions and how they can be used as arguments for other functions (or methods in C#) and how functional programs avoid side-effects (that is modifying a global program state).

Next we’ve looked shortly at the F# language by demonstrating several “Hello world” examples and we demonstrated some of the functional concepts in F# and how a similar thing can be achieved in C#. We’ve looked at recursion, Func delegate in C# and functions in F#.

Finally we’ve discussed functional programming from an architectural point of view. I wrote that when developing functional programs, we first think about the data structures and operations that transform or analyze these structures and we’ve also seen that using immutable data structures is extremely useful for parallelizing the code. We also looked at language oriented development in F#. In particular we’ve seen that functions for working with lists can be viewed as a “language” with a vocabulary and grammatical rules and I also shortly demonstrated another “language”, which can be used for creating functional animations.

More information about functional programming in context of .NET can be found in my book Real-world functional programming in .NET, which reveals more connections between functional programming and C# 3.0 with LINQ as well as introduces the new functional F# language in a more detail.

References

The online resources and articles referenced from this greenpaper include the following:

• [1] Real-world Functional Programming in .NET. - Tomas Petricek
• [2] Official F# web site - Don Syme et al
• [3] F# in Visual Studio 2008 for free - Douglas Stockwell
• [4] F# Overview. - Tomas Petricek
• [5] Microsoft. Parallel Computing web site
• [6] Keep your multi-core CPU busy with F# - Tomas Petricek
• [7] Fabulous Adventures in Coding – Immutability - Eric Lippert
• [8] Building LINQ queries at runtime in F# - Tomas Petricek

F# community web sites

There are also many useful community resources on F# that are worth visiting if you’re interested in F#. First of all, there is a F# community web site [A] with forums and blogs. There is also an F# wiki [B] and various blogs on F# [C, D, E and F]. If you’re looking for examples that use F#, you can take a look at some open-source F# projects [G and H].

• [A] hubFS: THE place for F# - The F# community web site with blogs, forums, etc..
• [B] F# Wiki Homepage - F# Wiki started by Robert Pickering
• [C] Don Syme’s WebLog on F# and Other Research Projects - Blog written by the F# language designer Don Syme
• [D] Robert Pickering’s Strange Blog - Blog of one of the most active F# community members
• [E] Tomas Petricek - My blog on F# and various other topics
• [G] F# Samples - Contains code that demonstrate various F# language features
• [H] F# WebTools - Advanced project that allows writing client/server Ajax web applications entirely in F#
• [F] F# News and F#.NET Tutorials by Jon Harrop