F# Math (II.) - Using matrices for graph algorithms
In the previous article of this
series, we looked at complex and BigRational, which are two
numeric types that are available in F# PowerPack. Aside from these two, the PowerPack
library also contains a type matrix representing a two-dimensional matrix
of floating-point values.
In this article, you'll learn how to work with matrices in F#, using some of the functions provided by F# PowerPack. I'll demonstrate the library using an example that represents graphs using a, so called, adjacency matrix. If you're not familiar with this concept, you don't need to worry. It is quite simple and it will be clear once we look at an example. The matrix represents which vertices of a graph are connected with other vertices by an edge. Many of the standard operations on matrices are useful when working with adjacency matrix, so this tutorial will cover the following:
- Creating matrices from lists and using functions from the
Matrixmodule - Using slices to read or modify a part of matrix
- Performing standard operations with matrices such as transposition and matrix multiplication
- Using higher order functions for working with matrices
This article is a part of a series that covers some F# and F# PowerPack features for numerical computing. Other articles in this series discuss matrices, defining custom numeric types and writing generic code. For links to other parts, see F# Math - Overview of F# PowerPack.
Representing graphs using matrices
The folowing figure demonstrates how the adjacency matrix looks. It shows a graph with N vertices and its representation using an adjacency matrix of size N*N. A column of the matrix contains 1 if there is an edge connecting the two vertices (specified by the coordinates of the column). If there is no edge, then the table contains 0:
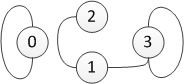
|
|
If you look at the adjacency matrix, you can see a few interesting facts. For example, the diagonal of the matrix contains 1 for vertices marked 0 and 3. This means that there are two edges from a vertex to itself. Also, the graph has two disconnected parts consisting of 1 and 3 vertices respectively. As a result, our matrix of size 4x4 could be composed from two matrices of size 1x1 and 3x3. The first one would contain only the column (0, 0) and the second would once contain columns from (1, 1) to (3, 3). All remaining columns in the composed matrix contain zeros, because there is no edge between the two separate components of the graph. The composition is demonstrated by the following matrix:
| vertex | 0 | 1-3 |
| 0 | m1 | 0 |
| 1-3 | 0 | m2 |
We'll see other interesting properties of the adjacency matrix later in the tutorial. First, let's take a look at various ways of constructing matrices, including a matrix representing the graph from the introduction.
Creating matrices
In order to work with matrices, you first need to add reference to PowerPack.dll.
Functionality for working with matrices is located in the namespace Microsoft.FSharp.Math,
so you'll also need to open this namespace. Note that the matrix type is not generic
and can contain only values of type float. In most of the cases, you'll want to
work with floats anyway, so this isn't a limitation. If you need to store other values in matrices,
you can use a generic version of the type, which will be discussed at the end of this article.
The following example shows the most straightforward way of creating matrices:
1: open Microsoft.FSharp.Math 2: 3: let m1 = matrix [ [ 1. ] ] 4: let m2 = matrix [ [ 0.; 1.; 1. ] 5: [ 1.; 0.; 0. ] 6: [ 1.; 0.; 1. ] ]
The two matrices created in the example correspond to the two parts of the matrix from the introduction. We'll use them later in this tutorial, so if you're going through the code in this tutorial, it may be useful to keep them in your source file.
Even though the code above looks like a special syntax for creating matrices, that's not the case. In
fact, matrix is an ordinary function that takes a sequence of sequences of floats and
constructs a matrix containing the values. The fact that matrix is an ordinary function means
that the parameter doesn't have to be a list literal. It can be a value or any other F# expression.
However, if you call matrix with a list of lists of non-equal lengths, you'll get a runtime error.
There are also several functions for creating matrices in the Matrix module:
1: Matrix.create 3 3 1.0 2: val it : matrix = matrix [ [1.0; 1.0; 1.0] 3: [1.0; 1.0; 1.0] 4: [1.0; 1.0; 1.0] ] 5: 6: Matrix.init 3 3 (fun i j -> 7: if i + j < 3 then 1.0 else 0.0) 8: val it : matrix = matrix [[1.0; 1.0; 1.0] 9: [1.0; 1.0; 0.0] 10: [1.0; 0.0; 0.0]]
The Matrix.create function creates a matrix of the specified size with all elements set
to the specified value. In our example, we use value 1.0. If we trated the matrix as an adjacency
matrix of some graph, the result would represent a complete graph that also contains an edge from
every vertex to itself.
The Matrix.init function is more complicated – it takes the required dimensions of
the matrix and a function. The function is called to calculate a value for each element in the
matrix. In our example, we return 1.0 only if the sum of current coordinates is less than 3. As a
result the upper left triangle in the matrix contains 1.0 and the rest contains 0.0.
The following table briefly reviews other functions that can be used for creating matrices:
| Matrix.identity |
int -> matrix
Creates a square matrix of the specified size that contains 1.0 on the diagonal and 0.0 otherwise. Created matrix is dense (meaning that elements are stored in a two dimensional array). |
| Matrix.initDense |
int -> int -> seq<int * int * float> -> matrix
Creates a dense matrix of the specified size. Then iterates over the given sequence and sets value of the columns specified by first two components of the tuple to the value (third component of the tuple). |
| Matrix.initSparse |
int -> int -> seq<int * int * float> -> matrix
Creates a sparse matrix of the specified size whose certain elements are set to the values specified by the sequence given as the third argument. Created matrix uses sparse representation, which is more memory-efficient for matrices containing mostly zeros. Some operations are not available for sparse matrices and they can be converted to dense representation using |
| Matrix.zero |
int -> int -> matrix
Creates a dense matrix of the specified size that contains 0.0 in every element. |
Working with matrices
Matrix is a mutable type, so it can be modified after it is created. When modifying matrices imperatively, the best approach is to do the modifications only once and then use the matrix as if it was immutable (e.g. after it is returned as a result from a function that is implemented using mutation). This way, you get good performance during the construction, but you can keep the rest of code referentially transparent.
Accessing matrix elements by index
The following listing shows a direct way of constructing adjacency matrix of size 4x4 from matrices that represent two parts of a graph as discussed in the introduction of this tutorial (though as we'll see later, there is a simpler way of doing this):
1: let m = Matrix.zero 4 4 2: val m : matrix = matrix [ ... ] 3: 4: m.[0, 0] <- m1.[0, 0] 5: val it : unit = () 6: 7: for i in 0 .. 2 do 8: for j in 0 .. 2 do 9: m.[i+1, j+1] <- m2.[i, j] 10: val it : unit = () 11: 12: m 13: val it : matrix = matrix [ [1.0; 0.0; 0.0; 0.0] 14: [0.0; 0.0; 1.0; 1.0] 15: [0.0; 1.0; 0.0; 0.0] 16: [0.0; 1.0; 0.0; 1.0] ]
The first command createS a matrix of size 4x4 whose elements are initialized to 0.0. Next, we
copy the content of matrices m1 and m2 (from the earlier section).
The matrix m1 contains only a single element, so we use direct assignment. For copying
elements of m2, we need to use two nested for loops. Once the elements are copied,
we ask F# Interactive to print the value of m. As you can see, the matrix is exactly
the same as the one in the figure from the introduction.
To look at one more example of working with elements of a matrix directly, let's write a piece of code that gives us a list of edges in the graph. This can be done by searching for 1.0 in the matrix. Note that we only need to search the triangle below the diagonal (including the diagonal), since the matrix is symmetric:
1: [ for i in 0 .. 3 do 2: for j in 0 .. i do 3: if (m.[i, j] = 1.0) then 4: yield i, j ] 5: val it : (int * int) list = [(0, 0); (2, 1); (3, 1); (3, 3)]
The upper bound of the nested loop is limited to the current value of i, so that we search
from the left border of the matrix to the diagonal only. If an element of the matrix contains 1.0, we
return the two vertex indices that specify an edge.
The use of nested loops for copying elements, earlier in this section, is unnecessarily complicated. The next section shows slices, which provide a nicer way of solving the problem.
Accessing parts of matrix using slices
Slices are similar to indices, but instead of specifying individual elements, they allow us to specify a range. The result is a matrix containing a part of the original matrix. Slices can be used not only for reading parts of matrix, but also to replace a part of matrix with another matrix.
For example, to remove the edge 4 from the original graph, we can take only the first three columns and three rows of the original matrix:
1: m.[0 .. 2, 0 .. 2] 2: val it : Matrix<float> = matrix [ [1.0; 0.0; 0.0] 3: [0.0; 0.0; 1.0] 4: [0.0; 1.0; 0.0] ]
The syntax of slices is similar to accessing elements of a matrix using indices. The only difference
is that in place of a single number (an index), we now write a range such as 0 .. 2. The
result of accessing a slice is a new matrix specified by the slice. If we look at the result, we can
see that by removing the vertex 4 from the graph, we get a graph with 3 vertices and only 2 edges (one
leads from vertex 1 to itself and one connects vertices 2 and 3).
Slices can be used for modifying the matrix as well. The following example shows a more elegant way of constructing the adjacency matrix for the entire graph from adjacency matrices of two disconnected parts:
1: let m = Matrix.zero 4 4 2: m.[0 .. 0, 0 .. 0] <- m1 3: m.[1 .. 3, 1 .. 3] <- m2
In the first assignment, the range describes a matrix of size 1x1 and in the second one we're overwriting a matrix of
size 3x3. If the size of the range was incompatible with the size of the matrix on the right hand side,
we would get an exception. Also note that there is an important difference between writing
m.[0, 0] and m.[0 .. 0, 0 .. 0]. In the first case, we're accessing only a single element, so the type
of the expression is float. In the second case, we're accessing a part of matrix that happens to contain
only a single element. Nevertheless, the type of the expression is still matrix.
Performing operations with matrices
Next we look at a few standard operations for working with matrices that are available in F# PowerPack.
Just like functions for creating matrices, the operations that we'll discuss in this step are available
in the Matrix module. The following listing demonstrates first two of them:
1: m = Matrix.transpose m 2: val it : bool = true 3: 4: Matrix.trace m 5: val it : float = 2.0
The first command tests whether a transpose of a matrix m is the same as
the original matrix. The result is true, because the matrix is symmetric (at least for any
graph that is not oriented, meaning that edge from vertex 1 to 2 is the same as edge from vertex 2 to 1).
The second command calculates so-called trace of a matrix which is a sum of
elements on the diagonal. When working with adjacency matrix, this gives the
number of vertices such that there is an edge from the vertex to itself.
In our case, the result is 2, because there is a value 1.0 at indices
[0, 0] and [3, 3], which correspond to edge from vertex 1 to 1 and
from 3 to 3 respectively.
The next example calculates the number of edges in the matrix. The fact that the matrix is symmetric means that some edges will appear twice in the matrix. To get the number of unique edges, we need to count only elements in the triangle over (or below) the diagonal, including the diagonal. The following example shows how to do that using two standard library functions:
1: m |> Matrix.mapi (fun i j value -> 2: if i > j then 0.0 else value) 3: |> Matrix.sum 4: val it : float = 4.0
The Matrix.mapi function can be used to calculate a new value for every element
in the matrix based on the index of the element and the original value. As most of the standard
functions for working with matrices, it returns a newly created matrix as the result. In the
example above, we replace all elements below the diagonal with zero. As a next step of the
processing, we sum all elements of the newly created matrix, which gives us the number of edges.
Other operations
We'll conclude this section with a brief review of several useful functions and operators for working with matrices provided by the F# PowerPack. The following table gives a few examples including a few groups of similar functions.
Point-wise operationsMatrix.cptMaxMatrix.cptMinOperators: + and .*
|
matrix -> matrix -> matrix
These functions and operators perform a binary operation on corresponding elements of two
matrices (of the same size) given as arguments and return the result in a new matrix. Functions
|
Logical aggregationMatrix.forallMatrix.exists |
(float -> bool) -> matrix -> bool
Functions implement quantification over all elements of the matrix. The function |
In-place operationsMatrix.inplaceAddMatrix.inplaceSub |
matrix -> matrix -> unit
These functions perform in-place addition and subtraction of matrices, storing the result in the first matrix and returning unit as the result. |
General aggregationMatrix.fold |
('a -> float -> 'a) -> 'a -> matrix -> 'a
Folds all elements into a single value. The function takes an aggregation function, initial state
and a matrix to be folded. The aggregation function is called for all elements of the matrix. The
variant |
General projectionMatrix.map |
(float -> float) -> matrix -> matrix
Applies the specified projection function to every element of the input matrix, storing the results
in a newly created matrix. The variant |
Reachability using matrix multiplication
One of the most important operations that can be done with matrices is matrix multiplication. I won't explain how matrix multiplication works in this tutorial, but I'll show you how to use it.
Matrix multiplication is quite useful when working with adjacency matrices. Another way of looking at adjacency matrix is that it specifies number of path of length 1 between each two vertices. If we multiply the adjacency matrix with itself, we'll get a number of paths of length 2 and so on. The listing shows what we get as the result:
1: m*m 2: val it : Matrix<float> = matrix [ [1.0; 0.0; 0.0; 0.0] 3: [0.0; 2.0; 0.0; 1.0] 4: [0.0; 0.0; 1.0; 1.0] 5: [0.0; 1.0; 1.0; 2.0] ]

The figure on the right (repeated from the introduction) shows the graph represented by
matrix m. What do the values in m*m represent? The value m.[1, 1]
gives us the number of paths between the vertex marked 1 and itself. The number 2.0 means that there are
two distinct paths. We can go from the vertex 1 to either 2 or 3 and then back, which gives us two
distinct paths. Another interesting fact is that there is no path of length 2 from vertex 2 to 1 (or
the other way round). They are connected by a direct edge, but a path of length 2 would need to
contain one more edge and there is no way to add this edge.
We can use matrix multiplication repeatedly to find which of the vertices are unreachable from which other vertices. We'll simply construct a matrix whose elements represents the number of paths of length 1, 2, ..., n and then find all zeros in the matrix. To find indices of elements containing zero, we can use the following function:
1: let collectUnreachable paths = 2: paths |> Matrix.foldi (fun i j st value -> 3: if (value <> 0.0) then st else (i, j)::st ) [] 4: val collectUnreachable : matrix -> (int * int) list
The function is implemented using Matrix.foldi, which iterates over all elements of the
matrix and accumulates some state during the iteration. We use empty list as an initial state. The
aggregation function gets indices of the element, the list of indices accumulated so far and the value
of the current element. If the value is zero, then we add the current indices to the list, otherwise
we simply return the original state.
The following listing uses the function to find vertices that are unreachable using a path of length one and also vertices which are unreachable using arbitrarily long path (the longest possible path that doesn't follow a single edge repeatedly in a graph with four vertices would have a length 3, so we only need to check for paths of this length):
1: collectUnreachable m 2: val it : (int * int) list = 3: [ (3, 2); (3, 0); (2, 3); (2, 2); (2, 0); 4: (1, 1); (1, 0); (0, 3); (0, 2); (0, 1) ] 5: 6: let paths = m + m * m + m * m * m 7: val paths : matrix = matrix [ ... ] 8: 9: collectUnreachable paths 10: val it : (int * int) list = [ (3, 0); (2, 0); (1, 0); (0, 3); (0, 2); (0, 1) ]
In the first case, we call the function with the original matrix as an argument and we get pairs of vertices
that are not directly connected by a path. Note that we didn't do anything to remove symmetric vertices,
so the result contains for example both (2, 3) and (3, 2). Next, we construct the matrix paths
by adding the original adjacency matrix, m multiplied by m and m
multiplied by m two times. This gives us a matrix indicating number of paths of lengths
1, 2 and 3. If we find unreachable vertices in this matrix, we can see that we cannot get from
the vertex 0 to any other vertex, but all other vertices are connected. This is exactly what
you would expect after looking at the figure with the graph.
Introducing generic matrix
So far, we've been working only with matrices that store elements of type float. This is the
most frequently needed type of matrix and you'll probably work with it most of the time in F#. To
make the most common case convenient, F# provides the matrix type. However, it is also possible
to create a matrix containing any other type such as int, decimal, or any
custom numeric type that provides numeric operations.
In the following two listings, we'll look at a brief example that re-implements some of the
functionality discussed earlier in this tutorial using a generic matrix. We'll use integers instead
of floats to represent the number of paths between two vertices. First, we'll need to create a
generic matrix. This can be done using functions from the Matrix.Generic module. To make the
module more easily accessible, we'll first declare a module alias:
1: module MatrixG = Matrix.Generic
The function matrix works only with floating point numbers. Luckily, we can use a
function MatrixG.ofSeq, which does exactly the same thing, but works for any type. Then
we can use all the familiar matrix operations we've seen earlier:
1: let m = Matrix.Generic.ofSeq [ [ 0; 0; 1 ] 2: [ 0; 1; 0 ] 3: [ 1; 0; 1 ] ] 4: val m : Matrix<int> = matrix [ ... ] 5: 6: let paths = m + m * m 7: val it : Matrix<int> = matrix [ [1; 0; 2 8: [0; 2; 0 9: [2; 0; 3] ]
The listing first creates a matrix containing integers and then uses point-wise addition
of matrices and matrix multiplication to get a matrix that represents number of paths of length
1 or 2 between vertices. It is worth noting that we could create matrix containing non-numeric
values such as string. This is possible, but some operations such as + and *
would throw an exception, because the string type doesn't support them. However, some
other operations such as map or fold work for matrices of any types.
Most of the functions from the Matrix module are also available in
Matrix.Generic. The last example shows how to find combinations of unreachable
vertices in an adjancency matrix containing integers:
1: paths |> MatrixG.foldi (fun i j st value -> 2: if (value = 0) then (i, j)::st else st) [] 3: val it : (int * int) list = [(2, 1); (1, 2); (1, 0); (0, 1)]
The code is exactly the same as the one we wrote earlier with the exception that we're using
foldi function from the MatrixG module. If we look at the result, we
can see that there is no connection between the vertex 1 and any other vertex in the matrix.
Summary
This article demonstrated how to use the matrix type from F# PowerPack to
implement graph algorithms using adjacency matrix. We looked at functions for creating matrices,
accessing matrix elements and slices, as well as at some of the operations that F# PowerPack
provides for working with matrices.
The matrix type supports most of the standard operations that one would
expect (such as matrix multiplication), but the implementation is not optimized. This means that
it may is a good way for representing graphs or solving other problems that are not
computationally intensive. However, the type is not suitable for highly-efficient numeric
calculations.
If you're interested in performance, then you can take a look at
F# MathProvider [4], which provides efficient implementation of
some matrix operations using wrappers for (native) Blas and Lapack. Alternatively,
there is a wide range of numeric libraries suitable for F# [3], most importantly
the open-source project Math.NET Numerics [5].
References & Links
- [1] F# PowerPack (source code and binary packages) - CodePlex
- [2] Numeric Computing - Real World Functional Programming on MSDN
- [3] Numerical Libraries for F# and .NET - Real World Functional Programming on MSDN
- [4] F# MathProvider - CodePlex
- [5] Math.NET Numerics - Open-source Mathematics for .NET
Published: Wednesday, 9 November 2011, 1:46 AM
Author: Tomas Petricek
Typos: Send me a pull request!
Tags: functional, f#, math and numerics