The theory behind covariance and contravariance in C# 4

In C# 4.0, we can annotate generic type parameters with out and in annotations to specify whether they should behave covariantly or contravariantly. This is mainly useful when using already defined standard interfaces. Covariance means that you can use IEnumerable<string> in place where IEnumerable<object> is expected. Contravariance allows you to pass IComparable<object> as an argument of a method taking IComparable<string>.

So far, so good. If you already learned about covariance and contravariance in C# 4, then the above two examples are probably familiar. If you're new to the concepts, then the examples should make sense (after a bit of thinking, but I'll say more about them). However, there is still a number of questions. Is there some easy way to explain the two concepts? Why one option makes sense for some types and the other for different types? And why the hell is it called covariance and contravariance anyway?

In this blog post, I'll explain some of the mathematics that you can use to think about covariance and contravariance.

Covariance and contravariance in C#

Let's say that we have a hierarchy of classes as shown in the diagram on the right. All types are subclasses of the .NET object type. Then we have Animal which has two subclasses Cat and Fish and finally, there is also some other .NET type Random.

Covariance

Let's start by looking what covariance means. Assuming that every Animal has a Name, we can write the following function that prints names of all animals in some collection:

void PrintAnimals(IEnumerable<Animal> animals) {
  for(var animal in animals)
    Console.WriteLine(animal.Name);
}

It is important to note that IEnumerable<Animal> can be only used to read Animal values from the collection (using the Current property of IEnumerator<Animal>). There is no way we could write Animal back to the collection - it is read-only. Now, if we create a collection of cats, can we use PrintAnimals to print their names?

IEnumerable<Cat> cats = new List<Cat> { new Cat("Troublemaker") };
PrintAnimals(cats);

If you compile and run this sample, you'll see that the C# compiler accepts it and the program runs fine. When calling PrintAnimals, the compiler uses covariance to convert IEnumerable<Cat> to IEnumerable<Animal>. This is correct, because the IEnumerable interface is marked as covariant using the out annotation. When you run the program, the PrintAnimals method cannot cause anything wrong, because it can only read animals from the collection. Using a collection of cats as an argument is fine, because all cats are animals.

Contravariance

Contravariance works the other way than covariance. Let's say we have a method that creates some cats and compares them using a provided IComparer<Cat> object. In a more realistic example, the method might, for example, sort the cats:

void CompareCats(IComparer<Cat> comparer) {
  var cat1 = new Cat("Otto");
  var cat2 = new Cat("Troublemaker");
  if (comparer.Compare(cat2, cat1) > 0) 
    Console.WriteLine("Troublemaker wins!");
}

The comparer object takes cats as arguments, but it never returns a cat as the result. You could say that it is a write-only in the way in which it uses the generic type parameter. Now, thanks to contravariance, we can create a comparer that can compare animals and use it as an argument to CompareCats:

IComparator<Animal> compareAnimals = new AnimalSizeComparator();
CompareCats(compareAnimals);

The compiler accepts this code because the IComparer interface is contravariant and its generic type parameter is marked with the in annotation. When you run the program, it also makes sense. The compareAnimals object that we created knows how to compare animals and so it can certainly also compare two cats. A problem would be if we could read a Cat from IComparer<Cat> (because we couldn't get Cat from IComparer<Animal>!), but that is not possible, because IComparer is write-only.

Categories and classes

Like surprisingly many other programming language concepts, the terms covariance and contravariance come from an abstract branch of mathematics called category theory. Category theory has a reputation for being very abstract - in fact, the category theory wikipedia page mentions that some call it "general abstract nonsense". The theory starts with a fairly simple definition and then builds more and more abstractions on top of the previous layer, so it is easy to lose track. However, we do not need to go very far to explain covariance and contravariance.

Category of classes

Let's take another look at the diagram that relates different classes in our example (beginning of the previous section). We can read an arrow from A to B in the diagram as it is possible to use A where B is expected. For example, it is possible to use Cat where an Animal is expected and it is possible to use Animal where an object is expected.

To make the diagram complete, we need to add a couple of arrows (see the new version on the right).

• Firstly, any class A can be used where a class A is expected (obviously!), so we need to add an arrow from each class to itself. These are showed as dotted lines.

• Secondly, if we can use class A where B is expected and B where C is expected, then we can also use A where C is expected. This means that if there is an arrow from Cat to Animal and from Animal to object, we should also draw an arrow from Cat to object. These are shown as dashed lines.

What I described in this section is essentially what category theorists call a category - objects connected with arrows that satisfy the two properties above. Let's look at the definition more formally...

Definition of category

A category is defined as a set of objects together with arrows between them. You can visualize it as a diagram with dots or boxes (representing objects) and arrows between them. We can compose arrows between objects, so if we have an arrow from A to B and an arrow from B to C, there is also an arrow from A to C (which can be constructed from the two arrows). In addition, there are two requirements about arrows:

• For every object A, there is an arrow from A to A (this is called identity).

• If we have arrows A -> B, B -> C and C -> D, then composing A -> B with B -> C and then composing the result with C -> D is the same arrow as composing B -> C with C -> D first and then adding A -> B at the beginning (this is called associativity).

Category theory is very abstract, because it does not tell us anything about the objects and arrows involved. They could be just anything. You can create a category by taking numbers and drawing arrow between a and b if a is greater than or equal to b, but you can also create a category from classes and draw arrows where a class can be used in place of another.

Functors and depth in hierarchy

There is one more idea from category theory that we need to understand covariance and contravariance and that is a functor. Let's say that we want to count the depth of the inheritance for objects in our class hierarchy. For example, object has depth zero; Animal and Random both have a single parent object. Finally, Fish and Cat both have depth two, since they have parent Animal, which has another parent object.

We can draw this as a transformation from our category of classes to a category of numbers - that is, a category with numbers 1, 2, 3, ... and an arrow between a and b if a >= b:

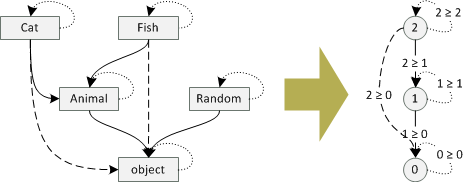
To be completely precise, we need to map objects as well as arrows of the category.

• For objects the mapping is as described above: object is mapped to 0; Animal and Random are mapped to 1; finally Cat and Fish are mapped to 2.

• For arrows the mapping maps an arrow representing the inheritance relation to an arrow that "proves" that the parent is actually a parent (and shows how far in the hierarchy it is). So, the arrows from Cat to object and from Fish to object are mapped to the arrow 2 >= 0 (and so on). Identity arrows (i.e. from Random to Random) are mapped to arrows a >= a (for Random, this is the arrow 1 >= 1).

Note that the mapping has some interesting properties. All identity arrows on the left are mapped to the identity arrows on the right. Also, if we compose an arrow on the left (i.e. from Fish to Animal with an arrow from Animal to object) and then map it, we get the same arrow as if we first mapped the two arrows and then composed the result (arrow 2 >= 1 with an arrow 1 >= 0, which composes to an arrow 2 >= 0).

Definition of a functor

The mapping that we just described is exactly what category theorists call functor. To make this blog post fancier, let's look at the formal definition. Assuming that we have two categories C and D (i.e. our classes and numbers) a functor F from C to D is a mapping that:

• to each object from C assigns an object from D; if A is an object in C, we write F(A) for the assigned object in D (in our example, F(Cat) = 2 and F(object) = 0).

• to each arrow from A to B in category C, a functor assigns an arrow from F(A) to F(B) in the category D (in our example, this is simple, because we only have a single arrow between two numbers; in general there may be multiple arrows - to demonstrate the concept, given an arrow from Cat to Animal, we assign it an arrow from 2 to 1, which is an arrow labelled with 2 >= 1).

In addition, two conditions must hold. Firstly, the arrow assigned to the identity arrow (arrow from A to A in category C) needs to be the identity arrow of the object F(A). Secondly, if we compose arrows and then map the composed arrow, the result should be the same as if we first map the arrows and then compose the result. The two conditions are exactly the same as the ones I mentioned at the end of the previous section. Although these are important in theory, we don't need to worry about them (because I will not cheat and when I say that something is a functor, it will actually obey these two laws!)

Functors and generic types

So far, I explained what a functor is and we looked at an example - mapping from a category of classes to a category of numbers that assigns the depth in a class hierarchy to every class. The example was interesting, because it mapped more complex structure (tree of classes) to a flat structure (just ordered numbers). In general, functors can do fairly complicated things. To explain covariance and contravariance, we need to look at pretty simple functors though.

Covariant functors

The definition of functor that I described earlier is actually a covariant functor. The covariant label means that it keeps the same orientation of arrows when mapping them. To an arrow A -> B, the functor assigns an arrow F(A) -> F(B). So, how does this relate to covariant generic types?

We can understand IEnumerable<T> as a functor that takes classes such as Cat or Animal to enumerable interfaces IEnumerable<Cat> and IEnumerable<Animal>, respectively:

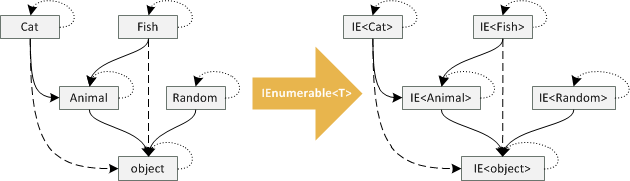
The mapping between objects is quite simple. Given a type named Cat, the mapping gives us back a type IEnumerable<Cat> (and similarly for all other types). The mapping of arrows is also straightforward. If we have a type Cat that can be used in place of Animal (that is, we have an arrow Cat -> Animal), then the arrow is mapped to an arrow between IEnumerable<Cat> and IEnumerable<Animal>. This means that the mapping preserves orientation of arrows and so we can use IEnumerable<Cat> where an IEnumerable<Animal> is expected!

Okay, I bet you can already guess what is going to happen with the picture when we look at contravariant generic types such as IComparable...

Contravariant functors

The definition of functor that I showed earlier is actually a definition of covariant functor, but category theory also defines contravariant functors. The only difference is that contravariant functor reverses the orientation of all arrows. So, if we have a contravariant functor G from category C to D, it means that:

• to each object from C assigns an object from D (same as previously)

• to each arrow from A to B in category C, a functor assigns an arrow from F(B) to F(A) in the category D (note that the arrow between F(B) and F(A) is now in the opposite direction!)

Let's look at an example. The IComparer<T> type is a contravariant functor. For objects, the mapping is quite simple. Given Animal, the functor gives us a type IComparer<Animal> (and similarly for other types). However, the mapping on arrows is interesting. If we have an arrow from Cat to Animal (saying that Cat can be used where Animal is expected), the mapped arrow is reversed, so we get an arrow from IComparer<Animal> to IComparer<Cat>. This corresponds to the C# example in the first section - we can use comparer on animals to compare cats. The following diagram shows how contravariant functor reverses arrows in our category of classes:

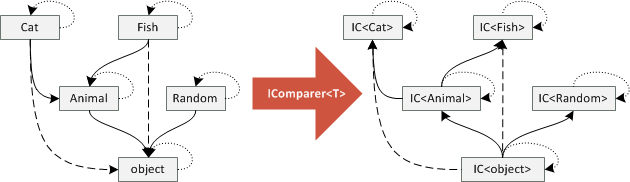
The diagram tells us some interesting things. By reversing the arrows, there is now an arrow from IComparer<object> to any other IComparer in the diagram. This means that we can use IComparer<object> to compare anything! (In the covariant case, any IEnumerable could have been used as an argument to method taking IEnumerable<object>.) Also, there is no terminal object so we cannot write a method that will take any IComparer as an argument. (This does not really have any practical implications, but it is interesting nevertheless!)

Summary

If you followed the article up to this point, then congratulations and thanks for staying with me! You learned quite a few concepts from general abstract nonsense branch of mathematics, but I hope you could see that they nicely correspond to features in C# 4.0. We started by looking at the definition of category and how it corresponds to class hierarchies (with classes as objects and inheritance as arrows). Then we looked at functors and how covariant functors model covariant generic types like IEnumerable<T> and contravariant functors model contravariant types like IComparer<T>.

Why category theory matters?

This may be an interesting intelectual exercise, but why should we care? Firstly, I think that reading this article gives you a better intuition about covariance and contravariance, which are quite hard to understand concepts.

If you're just going to use C# 4, then you don't really need to worry about category theory. If you do something wrong, the compiler will tell you (and will keep telling you until you get it right). Luckilly, the C# language designers understood the theory for us! However, even if you're not designing a language, knowing the theory might help you understand complex C# code. For example, take a look at the following example:

static void CallWithPrinter(Action<Action<Animal>> animalGenerator) {
  animalGenerator(animal => Console.WriteLine(animal.Name));
}

The method takes an Action delegate (which is contravariant) that takes another Action delegate as the input and does something. This nested delegate accepts any argument of type Animal. The method invokes the delegate and gives it a lambda function that takes an animal and prints its name. Now, the question is, can we use Action<Action<Cat>> as an argument to CallWithPrinter?

Action<Action<Cat>> catGenerator = handler => handler(new Cat("Otto"));
CallWithPrinter(catGenerator);

The sample creates a lambda function that takes a handler of type Action<Cat> and calls it with a sample cat as an argument. If you try to write this code in C# 4, it will compile and run fine. Why is that the case? Because we are applying Action<T> delegate two times and so we reverse the arrows twice! See the following diagram:

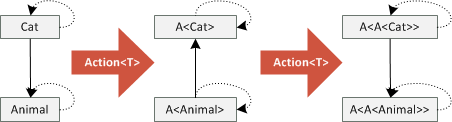
Understanding why the previous code snippet is correct just using the C# specification could be quite hard. The example is quite simple, so you might intuitively expect it to work (and hope that the compiler agrees), but intuition can be sometimes tricky. Understanding the theory gives you a powerful tool that you can use to better understand what is going on, even in complicated situations that combine covariant and contravariant types in crazy ways!