The mythology of programming language ideas

If you read a about the history of science, you will no doubt be astonished by some of the amazing theories that people used to believe. I recently finished reading The Invention of Science by David Wootton, which documents many of them (and is well worth reading, not just because of this!) For example, did you know that if you put garlic on a magnet, the magnet will stop working? Fortunately, you can recover the magnet by smearing goats blood on it. Giambattista della Porta tested this and concluded that it was false, but Alexander Ross argued that our garlic is perhaps not so vigorous as those of ancient Greeks.

You can just laugh at these stories, but they can serve as interesting lessons for any scientist. The lesson, however, is not the obvious one. Academics will sometimes read those stories and use them to argue against something they do not consider scientific - arguing that it is like believing that garlic break magnets.

This is not how the analogy works. What is amazing about the old stories is that the conclusions that now seem funny often had very solid reasoning behind them. If you believed in the basic assumption of the time, then you could reach the same conclusions by following fairly sound reasoning principles. In other words, the amazing theories were scientific and entirely reasonable. The lesson is that what seems a completely reasonable idea now, may turn out to be wrong and quite hilarious in retrospect.

In this article, I will look at a couple of amazing theories that people believed in the past and I will explain why they were reasonable given the way of thinking of the time. Along the way, I will explore some of the ways of thinking that we use today about programming and computer science and why they might appear silly in the future.

Episteme and scientific paradigms

The idea that scientific theories depend on basic assumptions that can change over time is well established in philosophy of science. This is fundamentally why naive view of science fails to explain how science works - science is not as simple as one might think. There is a number of relevant ideas. Foucault's epsiteme is a way of thinking during a specific historical era and is foundation that enables any sort of reasoning; Kuhn's scientific paradigms determine what is considered a scientific question and methods for answering scientific questions. Finally, Lakatos' concept of research programme determines normal ways of doing science among a smaller group of scientists.

I wrote about episteme, paradigms and research programmes before, so I will not repeat everything here. The main point is that episteme and research paradigms change from time to time and this affects what we consider scientific. Some entities might survive a paradigm shift, but some may become meaningless. If this was not the case, old theories would perhaps seem outdated, but they would not look like something that no sane person could ever believe. With theories from the history of science, the paradigm shift has already happened and so we can laugh at them with the benefit of hindsight. With theories from programming or computer science, we can just speculate. Someone else will have to enjoy the retrospective view!

How can we understand the world

Putting yourself in the shoes of a herbalist from 17th century is not easy, but I hope you are now curious enough to try. How did herbalist learn about the effects of herbs? After that, I'll ask you to try putting yourself into the shoes of a computer scientist of 24th century trying to put himself or herself into the shoes of a computer scientist of 21st century...

Doctrine of signatures in medicine

The doctrine of signatures was a theory dating back to ancient Greece that was widely accepted in medicine of 16th and early 17th century. According to the theory, herbs that resemble various parts of body can be used to heal diseases affecting that part of the body. The following illustrations are from 1923 reconstruction of 16th century illustrations, drawn by the same della Porta who did the experiment with magnets and garlic.

It is a fascinating idea, but nobody (reasonable) would treat it as a scientific theory these days. If some of the herbs were actually helpful, we can explain that as post-hoc attribution. Somebody just kept looking at the plant in various ways until they found the hand (or other organ) they were looking for.

How could this ever made sense? People of the time believed that God created the world so that human can understand it. Given that people were (and still are) able to understand some aspects of the world, this sounds like something that a person of the time might reasonably accept. The way this was interpreted was that the world is full of signs that we can recognize. As Foucault explains in The Order of Things, the Renaissance episteme was characterized by looking for those signs to identify sympathies and antipathies (magnets just do not like garlic!)

The shape of the herb that makes the root look a bit like hand is a sign, waiting to be discovered by an observant natural historian. As you can see, the theory follows fairly logically from the accepted way of thinking of the time. Would it pass an unbiased experimental evaluation? No, it would not, but experimentation as we know it now simply was not a part of the way of scientific thinking back then.

Scientific knowledge in computer science

As you can see, the idea that herbs would heal organs that it resembles logically followed from the beliefs of the time. It only seems silly in retrospect. Now, let's have a look at some of the beliefs about programming and computer science of our time. I will write about programming languages, because that is my background, but you can find analogies in other areas. Which of the beliefs will appear silly in a few hundred years?

Computer scientists of the 21st century believes that they can understand programming languages in a number of ways. We can study properties of mathematical models, we can perform experiments and measure things, or we can do user studies. User studies are the least objective method, but it is important, because, in the end, programming languages are used by people. Measurements also have their issues, but if done well, they give us solid scientific knowledge. Studying mathematical properties gives us the most pure and infallible form of knowledge - mathematical truths!

This way of thinking influences much of the things researchers and, to some extent, people in the industry do. We write POPL papers about the perfect mathematical truths and people love to read them. In the industry, we also like to measure things when possible - be it number of GitHub stars, code coverage or a somewhat mysterious popularity of programming languages.

Yet, the perfect mathematical knowledge is often about a programming language that has three language constructs λ-abstraction, variables and application. They do exist in some languages used in practice, but do not capture the complexity of real programming. Doing empirical evaluation is also hard. You cannot realistically get two teams of the same skills develop and maintain the same enterprise system over several years using a functional and object-oriented language, respectively, to compare them. Work on evidence based programming languages can tell you that repeat is a better keyword for iteration than for.

No doubt, we can use these methods to learn more about programming. But it is likely that, at some point, the way of thinking about programming will transform through a paradigm shift. What will a computer scientist from 24th century think about our methods? The point of paradigms is that it is impossible to step out of them, so I have no good answer. However, given that many things in computer science and programming are interconnected in complex ways, the future computer scientist might laugh at our attempt to study things in isolation and completely ignore further associations. They might think that we miss the forest for the trees.

Is there a vague similarity between lambda calculus and your favorite programming language? Well then, the nice formal properties of the lambda calculus somehow make your favorite programming language superior!

The unreasonable effectiveness of mathematics

The unreasonable effectiveness of mathematics in the natural sciences is a famous article that reflects on how mathematics can often hint at further empirical advances in scientific theories. That is certainly sometimes the case, but not always...

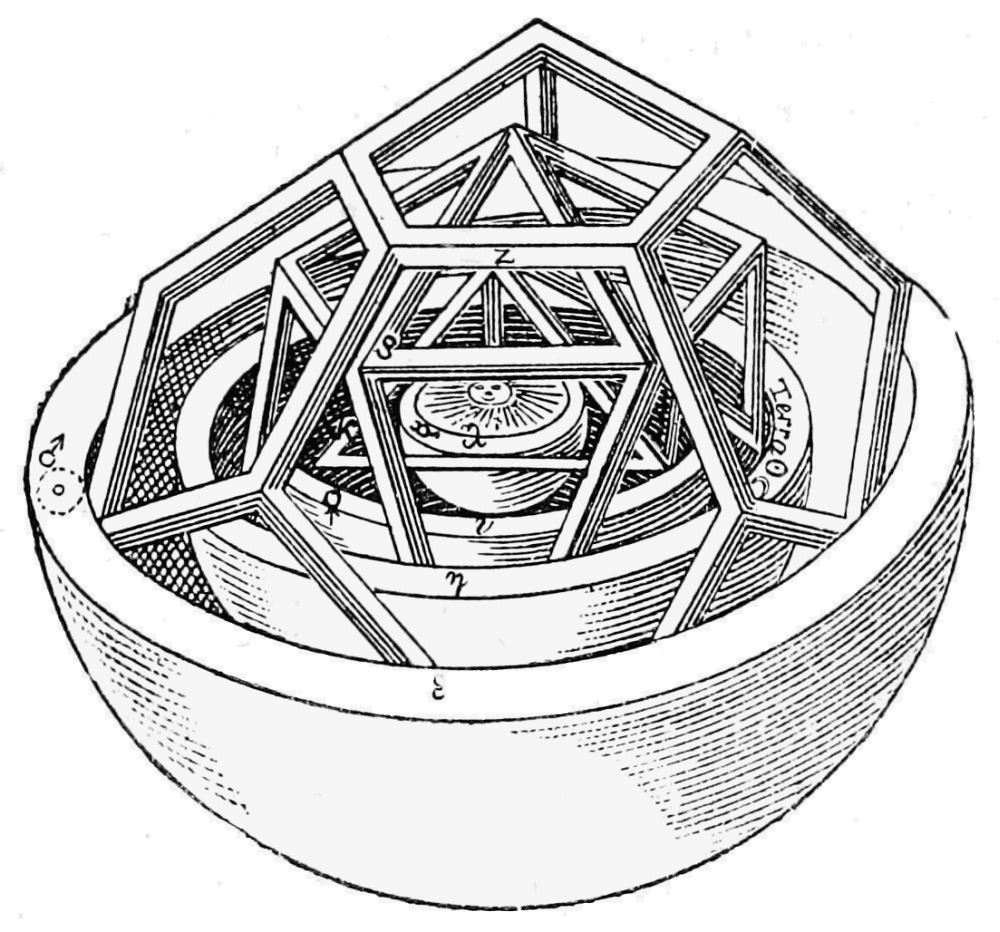
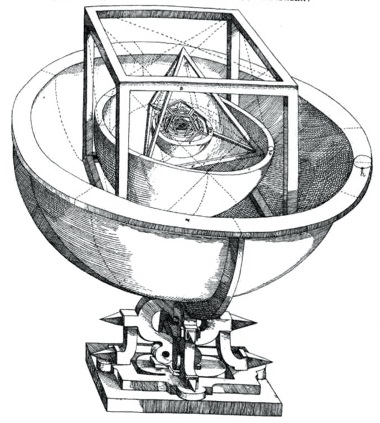
Johannes Kepler and platonic solids

Johannes Kepler is known for his astronomical work. He supported heliocentrism (replacing the Earth as the center of the universe with Sun) and believed that Sun was the primary power source for the movement of planets, later enabling Newton to formulate the theory of gravity. In Mysterium Cosmographicum, Kepler described his theory.

According to Kepler, the planets circle around the Sun in circles that are determined by spheres nested inside the five Platonic solids, which are then further nested inside the spheres. By ordering the polyhedra correctly, Kepler was able to propose model that quite closely described the movement of all the 6 known planets. The theory had the benefit that it provided an explanation for how the universe is constructed - this was not seen as a useful model, but an actual revelation of how the God constructed the universe.

Kepler's theory was based on Pythagorean mathematics, which had quite different way of thinking about numbers than we do today. They saw numbers as the ultimate substance from which the universe is constructed. For this reason, Kepler was constructing a reasonable theory - there are exactly five polyhedra and six planets, so his theory nicely linked the eternal mathematical truths with circular movement of planets. (Another belief of his time was that all movement in the sky is circular.)

Programming and category theory

In modern natural sciences, we mostly use mathematics as a tool for building models that describe our empirical observations. The paper on unreasonable effectiveness of mathematics in the natural sciences wonders what it is that makes mathematics so useful, but we do not take mathematical models for truth unless we have physical explanation - be it spheres bumping into each other or curvature of space-time.

This is not quite the case in computer science and in programming. Here, we quite happily follow Pythagorean number mysticism and believe that if something is created based on elegant mathematical construction, then it is somehow right. As the title of this section suggests, I think that category theory notions that got into programming like monads are nice examples of this way of thinking.

Of course, I'm not saying that mathematics is not useful in programming! The interesting lesson from Kepler is that we should try to understand why they are useful. In physics, mathematical models let us build models that fit observations, but we do not use mathematics as source of truth in the same way as Kepler did. Perhaps computer scientists of the 24th century will have better idea for why mathematics is useful in programming and they will look at some of our uses of mathematical constructs with admiration, but at other uses with amusement. But which ones will be which? That is, again, the billion dollar question! However, the work on understanding conceptual metaphors behind mathematics may tell us something important.

Scale of what we can imagine

My last example from the history of science will not involve just one fascinatingly wrong idea, but a story of how one wrong idea was transformed into another wrong idea. The latter was later adapted into what we find a reasonable theory nowadays.

Doctrine of preformationism and scaling revolution

As I mentioned, people believed that God created the world so that we can understand it. Back in 16th century, this meant that we can understand the world without unaided. This means that everything there is in the world was made to human scale - you can see all the animals and plants with your eye and all you see is all there is to see.

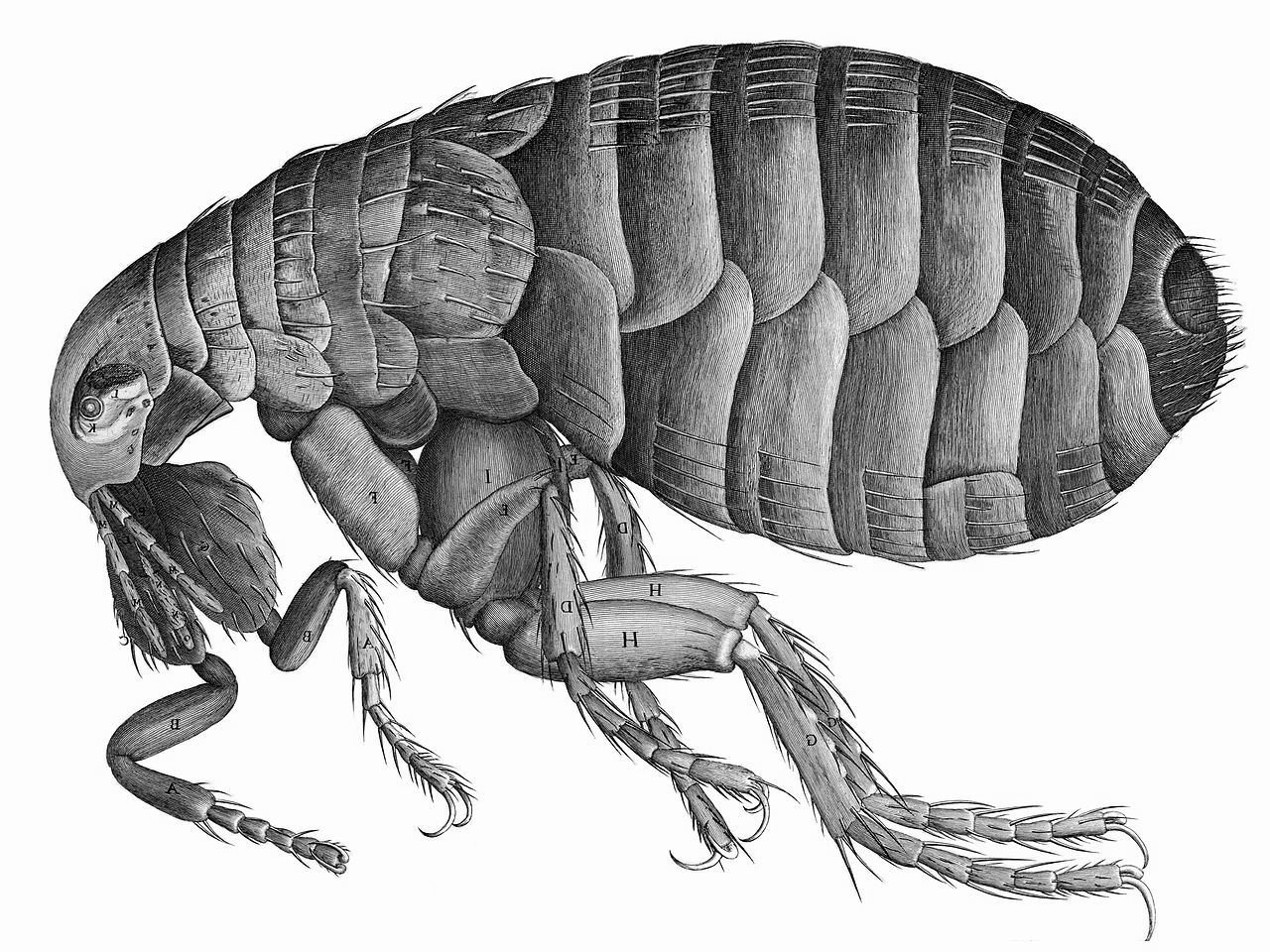
When microscope was invented, it took some time before people found it useful. At first, they did not believe that microscope can actually tell you something useful about the world. One of the first natural philosophers to study the nature through the lens of a microscope was Robert Hooke. He recorded his observations in Micrographia: or Some Physiological Descriptions of Minute Bodies Made by Magnifying Glasses. With Observations and Inquiries Thereupon, which included the picture of a flea, which I'm using as an illustration.

Looking at the details of a flea was not all though. If we look through the microscope, we can see a world that is as complex as our world. Jonathan Swift described the new way of thinking:

So nat'ralists observe, a flea
Has smaller fleas that on him prey;
and these have smaller fleas to bite 'em.
And so proceeds Ad infinitum.

The idea that a flea has smaller fleas is not just a poetical description of the wonders of a microscope. The scaling revolution made people think that there can really be an infinite chain of smaller and smaller fleas. An fascinating consequence of this way of thinking is the idea of preformationism.

The idea of preformationism is that large organism develop from smaller versions of themselves. A child is just a small human. Before the birth, a child is just a small homunculus hidden inside an egg or a sperm. The homunculus, in turn, contains yet smaller homunculi. In fact, the belief was that all created at the same time. The theory of preformationism was generally accepted since the scaling revolution of 17th century until 19th century when it was replaced by the cell theory.

The digital revolution and correctness

Is there something like the scaling revolution in computer science and how we think about programming? Perhaps, we can find an interesting similarity with the move from analog technology to digital computers. Analog technology has (not quite) an infinite range of values, while digital computers have only 1 or 0, also known as true or false.

The move to digital computers allowed a great number of developments in computing, but it also changed how we think about programs. With analog computers, a result of some computation can be close to the right one. With digital computers, there is no such thing - the result is either right or wrong. This makes perfect sense when we are talking about bits, but perhaps, just like the preformationists took the idea of scaling revolution a bit too far, we are also taking the absolute distinction too far.

For example, we think that "mostly functional programming" is unfeasible, because partially removing side-effects does not make a language pure. This is true from the absolutist digital perspective, but it does not seem to be the case in practice. Similarly, when computer scientists talk about program correctness, we use the absolute digital terms. A program is either correct, or it incorrect. Yet, in practice, there certainly is such a thing as only slightly broken software. Most software has some glitches, but it is still acceptable in practice. There is some recent interesting work on this idea, but it is still using a fairly binary distinction between acceptable and not acceptable.

The one area where the clear binary distinction does not seem to exist is in machine learning, so perhaps computer scientists of the 24th century will find a new way of thinking in terms of scale that is not quite analog and not quite digital. Can this be a bit like our current thinking about cells, which requires microscope, but does not proceed ad infinitum?

Conclusions

Before you ask, let me reassure you that I believe in science. I hope this is obvious to most readers, but for some reason, it seems important to say it nowadays. The amazing stories from the history of science do not illustrate that science does not work. Instead, they show how it works.

As we make more precise observations and conduct better experiments, we sometimes need to revise the way we think about the world. Some paradigm shifts make older theories look hilarious. The new way of thinking is based on different principles and so what appeared fairly logical in 16th century does not make much sense today. That said, many of the results from the old age get revised and become useful. Micrographia of Robert Hooke provided valuable observations, Kepler's measurements were useful and doctrine of signatures was useful as a mnemonic.

In the same way, our current ideas about computer science and programming are, no doubt, useful. Many of them are extremely useful and computer scientists of 24th century will refer to their proponents with much admiration. Inevitably, we also believe some theories that will appear as silly to future generations as some of the 16th century theories appear to us.

Science makes progress by using critical thinking. Scientific paradigms and research programmes explain that this is not always direct, because core assumptions take much longer to be revised than auxiliary theories. When thinking about computer science, we are also more likely to revise auxiliary theories. Thinking critically about the core assumptions from which our thinking follows is much harder. In this article, I wanted to illustrate some of the changes in core beliefs in the history of science and use those examples to suggest that even core beliefs that we have about computer science and programming may, at some point, be revised.

And what was the reason for believing that smearing garlic on a magnet will remove its powers? It seems that this was a typo in one of the ancient texts. Common belief in 16th century was that ancient philosophers were always right and knew everything there is to know, so nobody questioned this. Fortunately, believing that the authorities of our field are always right is something that we certainly would not do these days...

References

The stories from the history of science in this blog post are based on Wootton's book The Invention of Science, but if I misinterpreted something, it is entirely my fault! If you want to learn more, I put together a reading list on philosophy of science and computing. What Is This Thing Called Science? is a great introduction and The Structure of Scientific Revolutions is a classic book that introduced the idea of scientific paradigms; The Order of Things explains the idea of episteme and Renaissance way of thinking in terms of similitudes.

• David Wootton, The Invention of Science: A New History of the Scientific Revolution, Harper 2015
• Alan Chalmers, What Is This Thing Called Science?, Hackett 2013
• Thomas Kuhn, The Structure of Scientific Revolutions, University of Chicago Press 1962
• Michael Foucault, The Order of Things: An Archaeology of the Human Sciences, Vintage 1994