Composing Chrismas with F#

This blog post is a part of the awesome F# Advent Calendar (see the previous entry about writing algorithms in F# from Rick Minerich), so it inevitably needs a Christmassy theme. However, there is also going to be a serious theme for the blog post, which is domain-specific languages.

One of my favorite examples of Domain-Specific Languages is a simple OpenGL library that I wrote some time ago for composing 3D graphics in F#. You can see it in my NDC 2014 talk Domain Specific Languages, the functional way and I also used it for Solving Puzzles with F# earlier on this blog.

The nice thing about the library is that it is very simple, but is rich enough to demonstrate all the important concepts. In fact, the library is so easy to use that even 8 years old can do a talk about it. So, if you're spending Christmas with your family, perhaps you can go through this article with your children!

On the more serious note, I also want to show two important programming concepts:

• Composability is perhaps the most fundamental principle of functional programming. The idea is that we can build complex things by (correctly) composing smaller (correct) building blocks. This applies to computations, user interfaces as well as 3D objects.

• Layers of abstraction is another key theme. The idea is that you can build higher-level APIs on top of lower-level ones. For example, you can process F# lists using recursion (low-level), or using functions like filter and map built on top of that (high-level). You'll see the same thing with 3D objects.

Now, let's get started and build some 3D Christmas with F#!

Getting started with 3D

The first thing you'll need is to download the library and load it into F# Interactive. You could also create an application, but playing with the library interactively is more fun:

1: 
2: 
3: 
4: 
5: 
6: 
7: 

// Reference OpenTK library & functional DSL
#r "OpenTK.dll"
#r "OpenTK.GLControl.dll"
#load "functional3d.fs"
open System
open System.Drawing
open Functional3D

The library exposes a single module named Fun, so the best way to start exploring it is to type Fun. and see what your editor suggests. You can start, for example, with Fun.cone to create a cone. Then, select the expression and send it to F# Interactive to see the object.

Aside from primitive objects (Fun.cone, Fun.cube, Fun.sphere, etc.), the library gives us a couple of functions that transform an object - that is, they take a 3D object, apply some transformation and return a new one. We can, use them to take a cone, make it more spiky and move it (so that the base is in the center of the coordinates):

1: 
2: 
3: 

Fun.cone
|> Fun.scale (0.5, 0.5, 2.0)
|> Fun.translate (0.0, 0.0, -1.0)

Once the object appears, you can use the Q, W and A, S and Z, X keys to rotate the view.

Composing stars

The first thing we'll do in this blog post is that we'll create a (very Christmassy) star. To do that, we extend our language and add a new primitive that creates a spike. In a more techincal terms, we just write a function called spike:

1: 
2: 
3: 
4: 
5: 
6: 
7: 

/// Creates a single spike, starting from the
/// center of the world, rotated by `r` degrees
let spike r = 
  Fun.cone
  |> Fun.scale (0.5, 0.5, 2.0)
  |> Fun.translate (0.0, 0.0, -1.0)
  |> Fun.rotate (r, 0.0, 0.0)

The spike function wraps the code that we wrote in the previous snippet. It adds one more transformation, which rotates the spike using the specified number of degrees. Now, if we want to create a star with 4 spikes, we can just write:

1: 
2: 
3: 

( spike 0.0 $ spike 90.0 $ 
  spike 180.0 $ spike 270.0 )
|> Fun.color Color.Gold

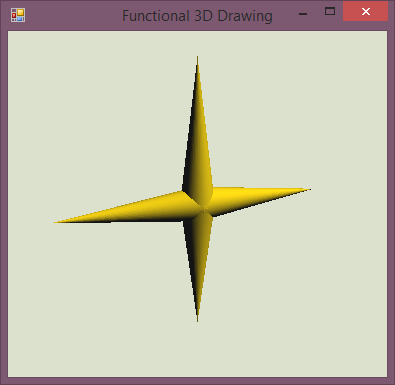
Here, we're using the $ operator, which comes from the functional 3D DSL to put multiple objects together - it simply renders multiple 3D objects in their original location (which is why we had to move the spikes earlier on).

Now, going back to the key concepts - what we are doing here is that we are composing a more complex primitive called spike from a simpler primitives. Also, we are rising the level of abstraction, because we can now create stars in terms of spikes, rather than just cones. You can easily change the code to create other stars by adding more spike calls.

So far, we also did not need almost any F# knowledge. We just used the |> operator and function calls. If we want to be more clever about creating stars, we can generate one using list comprehensions:

1: 
2: 
3: 
4: 

/// Represents a star with 12 spikes
let star =
  [ for r in 0.0 .. 30.0 .. 330.0 -> spike r ]
  |> List.reduce ($)

This snippet generates 12 spikes and then composes all of them into a single 3D object using the List.reduce function and the $ operator (which joins two 3D objects). The last step is to add some animation. The easiest way to do this is to write a function that takes the current time and returns an object. The following snippet changes the color and scaling of the star based on time:

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 

/// Creates a glowing star with changing color
let glowingStar time = 
  // Values varying between -96 .. +96 and 0.7 .. 1.3
  let phase = sin (time / 20.0) * 96.0
  let size = 1.0 + (0.3 * sin (time / 20.0))
  let clr = Color.FromArgb(255, 159+int phase, 64)
  
  // Change the color and scaling of a star
  star 
  |> Fun.color clr 
  |> Fun.scale (1.0, size, size) 
  |> Fun.rotate (90.0, 90.0, 90.0)

The library provides a primitive Fun.animate that takes a time-varying function and runs it. That is, the argument is a function float -> Drawing3D and the runner will call it repeatedly, incrementing the time at each step:

1: 
2: 
3: 
4: 

// Run this line to start the animation
let gs = Fun.animate glowingStar
// Run this line to stop the animation
gs.Cancel()

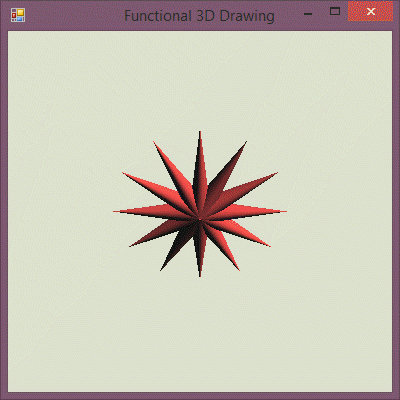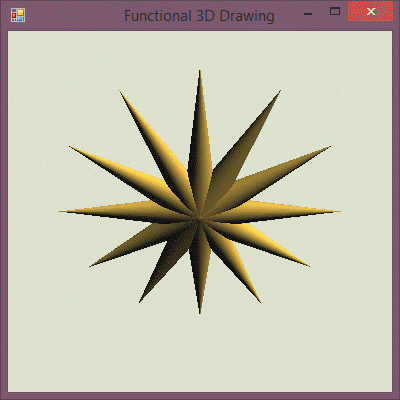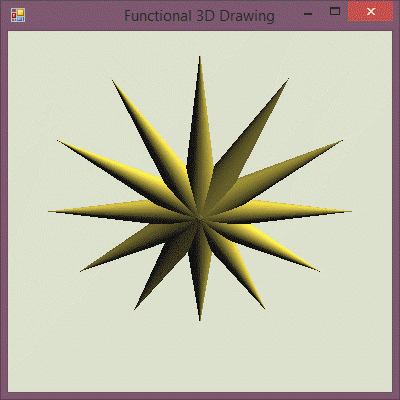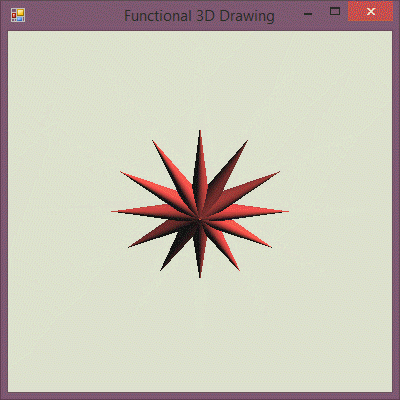
Stars are a good start, but we obviously need more than that to compose Christmas...

Composing Christmas trees

What we really need is a Christmas tree, decorated with a glowing star! We already have the star ready, so let's look at trees. To make our tree nicer, we're going to generate it using a variation of green shades, so let's start with a helper to get a random shade of green color:

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

let rnd = Random()
/// Returns a random shade of 
/// green color for the tree
let nextGreen() =
  Color.FromArgb
    ( rnd.Next(96), 
      rnd.Next(96, 168), 
      rnd.Next(64) )

To build a Christmas tree, we're going to simply add a number of cones on top of each other (to represent different levels of the tree). This is pretty much the same as composing stars from spikes. Create a list of cones, move and scale them appropriately and then put all of them together:

1: 
2: 
3: 
4: 
5: 
6: 
7: 
8: 

let tree = 
  [ for i in 0.0 .. 6.0 ->
      let w = 0.5 + i * 0.2
      Fun.cone
      |> Fun.color (nextGreen())
      |> Fun.scale (w, w, 0.4) 
      |> Fun.translate (0.0, 0.0, 0.30*i) ]
  |> List.reduce ($)

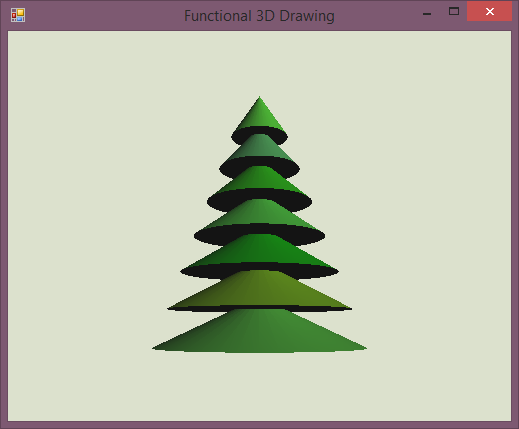
The only difficult thing about the above example is getting the constants right. Feel free to fiddle with the numbers to create different trees! Here, we're creating 7 levels and we are making them wider as we go. We also make each cone 0.4 high and move them so that they overlap by one quarter of a cone.

The other part of the tree that we need is a trunk. To build one, we're simply going to create a brown cylinder, make it narrow and longer and then move it to the bottom of the tree:

1: 
2: 
3: 
4: 
5: 

let trunk = 
  Fun.cylinder
  |> Fun.scale (0.2, 0.2, 1.0)
  |> Fun.color Color.Brown
  |> Fun.translate (0.0, 0.0, 1.9)

Now we are pretty much done with the tree! We can write just trunk $ tree, or we can also specify rotation and move it, so that it appears in the center of the window. If the rotation of the view (using keyboard keys) got out of control, you can call Fun.resetRotation():

1: 
2: 
3: 

(trunk $ tree)
|> Fun.rotate (90.0, 0.0, 0.0)
|> Fun.translate (0.0, 1.0, 0.0)

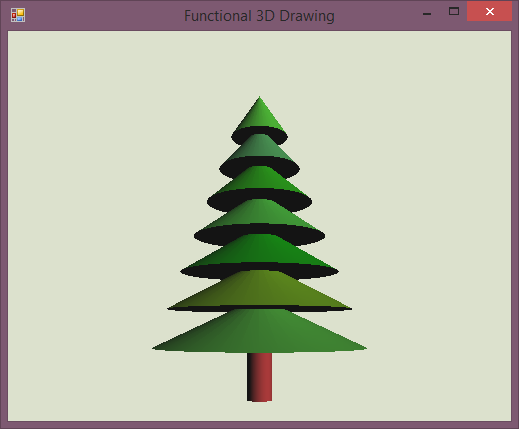
The beautiful thing about the Domain-Specific Languages approach that we are using here is not just the fact that we can build interesting things with just a few lines of code. The really nice thing is that we are rising the level of abstraction. Rather than talking about primitive objects, the code now talks about trunks, trees and stars. So, let's put the parts together...

Decorating tree

To put the glowing star on top of our tree, we need to write a function that takes the current time and returns a 3D object composed from tree (which does not change) and a glowing (time-dependent) star. We also need to make the star smaller and move it to the top:

 1: 
 2: 
 3: 
 4: 
 5: 
 6: 
 7: 
 8: 
 9: 
10: 
11: 
12: 
13: 

/// Tree with a glowing star on top
let treeWithStar time = 
  ( (trunk $ tree)
    |> Fun.rotate (90.0, 0.0, 0.0)
    |> Fun.translate (0.0, 1.0, 0.0) ) $
  ( glowingStar time
    |> Fun.scale (0.2, 0.2, 0.2)
    |> Fun.translate (0.0, 1.2, 0.0) )

// Run this line to start the animation
let ts = Fun.animate treeWithStar
// Run this line to stop the animation
ts.Cancel()

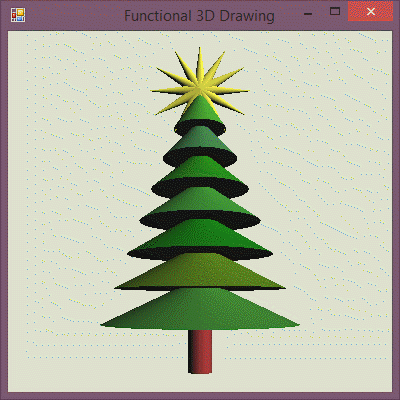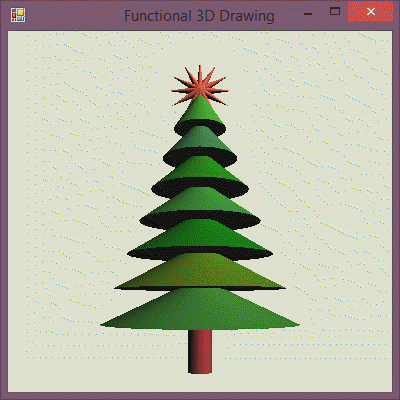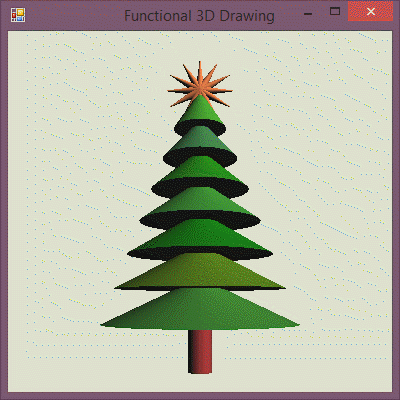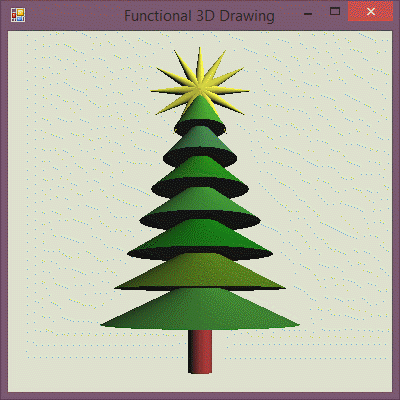
Summary

As I mentioned in the introduction, the library that I used in this blog post is easy enough that an 8 year old can use it. So, if you're spending some time over Christmas with kids, you can get the library and have some fun! The source code of this blog post is available on GitHub, including the text.

On the more serious note, I wanted to show you two important ideas. First, how composability makes it possible to easily build more complex things from simple ones (this is where the F# motto "simple code to solve complex problems" comes from). The other part is levels of abstraction - at the beginning, we only had low-level abstractions such as cones and cylinders. However, as we solved our specific problem, we ended up defining reusable, higher-level DSL primitives such as tree, star and trunk. These are not single-purpose - you can reuse the code for other problems that fall into the same Christmassy domain!